【题目】如图,在直角△ABC中,AB⊥BC,D为BC边上异于B、C的一点,以AB为直径作⊙O,并分别交AC,AD于点E,F.
(Ⅰ)证明:C,E,F,D四点共圆;
(Ⅱ)若D为BC的中点,且AF=3,FD=1,求AE的长.
参考答案:
【答案】(Ⅰ)证明:连结EF,BE,则∠ABE=∠AFE,因为AB是⊙O是直径, 所以,AE⊥BE,又因为AB⊥BC,∠ABE=∠C,
所以∠AFE=∠C,即∠EFD+∠C=180°,
∴C,E,F,D四点共圆.
(Ⅱ)解:因为AB⊥BC,AB是直径,
所以,BC是圆的切线,DB2=DFDA=4,即BD=2,
所以,AB= ![]() =2
=2 ![]() ,
,
因为D为BC的中点,所以BC=4,AC= ![]() =2
=2 ![]() ,
,
因为C、E、F、D四点共圆,所以AEAC=AFAD,
即2 ![]() AE=12,即AE=
AE=12,即AE= ![]()
【解析】(Ⅰ)连结EF,BE,说明AB是⊙O是直径,推出∠ABE=∠C,然后证明C,E,F,D四点共圆.(Ⅱ)利用切割线定理求解BD,利用C、E、F、D四点共圆,得到AEAC=AFAD,然后求解AE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆E:
 +
+  =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 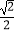 ,直线x+y+
,直线x+y+  =0与椭圆E仅有一个公共点.
=0与椭圆E仅有一个公共点.
(1)求椭圆E的方程;
(2)直线l被圆O:x2+y2=3所截得的弦长为3,且与椭圆E交于A、B两点,求△ABO面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形
 的三边长是公差为2的等差数列,且最大角的正弦值为
的三边长是公差为2的等差数列,且最大角的正弦值为 ,则这个三角形的周长是( )
,则这个三角形的周长是( )A. 18 B. 15 C. 21 D. 24
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(x+1)ex和函数g(x)=(ex﹣a)(x﹣1)2(a>0)(e为自然对数的底数).
(1)求函数f(x)的单调区间;
(2)判断函数g(x)的极值点的个数,并说明理由;
(3)若函数g(x)存在极值为2a2 , 求a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知直线l的参数方程为
 (t为参数,0<α<π),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ=
(t为参数,0<α<π),以原点O为极点,以x轴正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρ= 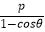 (p>0).
(p>0).
(Ⅰ)写出直线l的极坐标方程和曲线C的直角坐标方程;
(Ⅱ)若直线l与曲线C相交于A,B两点,求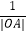 +
+ 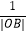 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(Ⅰ)求函数
 的最小值和最小正周期;
的最小值和最小正周期;(Ⅱ)已知
 内角
内角 的对边分别为
的对边分别为 ,且
,且 ,若向量
,若向量 与
与 共线,求
共线,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知三棱锥
 中,
中, 为
为 中点,
中点, 为
为 中点,且
中点,且 为正三角形.
为正三角形.(I)求证:
 平面
平面 ;
;(II)求证:平面
 平面
平面 ;
;(III)若
 ,求三棱锥
,求三棱锥 的体积.
的体积.
相关试题

