【题目】如今我们的互联网生活日益丰富,除了可以很方便地网购,网上叫外卖也开始成为不少人日常生活中不可或缺的一部分.为了解网络外卖在![]() 市的普及情况,
市的普及情况,![]() 市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
市某调查机构借助网络进行了关于网络外卖的问卷调查,并从参与调查的网民中抽取了200人进行抽样分析,得到下表:(单位:人)
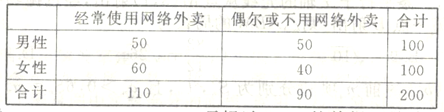
(1)根据以上数据,能否在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖的情况与性别有关?
市使用网络外卖的情况与性别有关?
(2)①现从所抽取的女网民中利用分层抽样的方法再抽取5人,再从这5人中随机选出3人赠送外卖优惠券,求选出的3人中至少有2人经常使用网络外卖的概率;
②将频率视为概率,从![]() 市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为
市所有参与调查的网民中随机抽取10人赠送礼品,记其中经常使用网络外卖的人数为![]() ,求
,求![]() 的数学期望和方差.
的数学期望和方差.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:

参考答案:
【答案】(1)不能在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖情况与性别有关.
市使用网络外卖情况与性别有关.
(2)①![]() ;②
;②![]() ;
;![]() .
.
【解析】试题分析:(1)计算![]() 的值,进而可查表下结论;
的值,进而可查表下结论;
(2)①由分层抽样的抽样比计算即可;
②由![]() 列联表,可知抽到经常使用网络外卖的网民的频率为
列联表,可知抽到经常使用网络外卖的网民的频率为![]() ,将频率视为概率,即从
,将频率视为概率,即从![]() 市市民中任意抽取1人,恰好抽到经常使用网络外卖的市民的概率为
市市民中任意抽取1人,恰好抽到经常使用网络外卖的市民的概率为![]() ,由题意得
,由题意得![]() .
.
试题解析:
(1)由列联表可知![]() 的观测值,
的观测值,![]()
![]() .
.
所以不能在犯错误的概率不超过0.15的前提下认为![]() 市使用网络外卖情况与性别有关.
市使用网络外卖情况与性别有关.
(2)①依题意,可知所抽取的5名女网民中,经常使用网络外卖的有![]() (人),
(人),
偶尔或不用网络外卖的有![]() (人).
(人).
则选出的3人中至少有2人经常使用网络外卖的概率为![]() .
.
②由![]() 列联表,可知抽到经常使用网络外卖的网民的频率为
列联表,可知抽到经常使用网络外卖的网民的频率为![]() ,
,
将频率视为概率,即从![]() 市市民中任意抽取1人,
市市民中任意抽取1人,
恰好抽到经常使用网络外卖的市民的概率为![]() .
.
由题意得![]() ,
,
所以![]() ;
;
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,直线
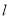 的参数方程为
的参数方程为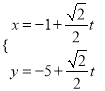 (其中
(其中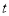 为参数),现以坐标原点为极点,
为参数),现以坐标原点为极点, 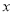 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线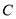 的极坐标方程为
的极坐标方程为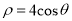 .
.(1)写出直线
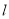 和曲线
和曲线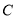 的普通方程;
的普通方程;(2)已知点
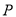 为曲线
为曲线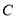 上的动点,求
上的动点,求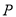 到直线
到直线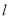 的距离的最小值.
的距离的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,其中
,其中 且
且 ,若
,若 ,
,  在
在 处切线的斜率为
处切线的斜率为 .
.(1)求函数
 的解析式及其单调区间;
的解析式及其单调区间;(2)若实数
 满足
满足 ,且
,且 对于任意
对于任意 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在数列{an}中,a1=
 ,且
,且 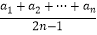 =nan(n∈N+).
=nan(n∈N+).
(1)写出此数列的前4项;
(2)归纳猜想{an}的通项公式,并用数学归纳法加以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知全集U=R,函数y=
 +
+  的定义域为A,函数y=
的定义域为A,函数y=  的定义域为B.
的定义域为B.
(1)求集合A、B.
(2)(UA)∪(UB). -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)的定义域为(0,+∞),f(2)=1,f(xy)=f(x)+f(y)且当x>1时,f(x)>0.
(1)判断函数f(x)在其定义域(0,+∞)上的单调性并证明;
(2)解不等式f(x)+f(x﹣2)≤3. -
科目: 来源: 题型:
查看答案和解析>>【题目】设0<a≤
 ,若满足不等式|x﹣a|<b的一切实数x,亦满足不等式|x﹣a2|<
,若满足不等式|x﹣a|<b的一切实数x,亦满足不等式|x﹣a2|<  ,求实数b的取值范围.
,求实数b的取值范围.
相关试题

