【题目】已知点![]() 是直线
是直线![]() 与椭圆
与椭圆![]() 的一个公共点,
的一个公共点,![]() 分别为该椭圆的左右焦点,设
分别为该椭圆的左右焦点,设![]() 取得最小值时椭圆为
取得最小值时椭圆为![]() .
.
(I)求椭圆![]() 的方程;
的方程;
(II)已知![]() 是椭圆
是椭圆![]() 上关于
上关于![]() 轴对称的两点,
轴对称的两点,![]() 是椭圆
是椭圆![]() 上异于
上异于![]() 的任意一点,直线
的任意一点,直线![]() 分别与
分别与![]() 轴交于点
轴交于点![]() ,试判断
,试判断![]() 是否为定值,并说明理由.
是否为定值,并说明理由.
参考答案:
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() 为定值1,理由见解析.
为定值1,理由见解析.
【解析】
试题分析:(Ⅰ)首先联立直线与椭圆方程,根据直线与椭圆有公共点利用判别式求得![]() 的取值范围,然后根据椭圆的定义即可求得椭圆
的取值范围,然后根据椭圆的定义即可求得椭圆![]() 的方程;(Ⅱ)首先设
的方程;(Ⅱ)首先设![]() ,
,![]() ,
,![]() ,然后根据
,然后根据![]() 结合点
结合点![]() 在椭圆上得到
在椭圆上得到![]() 关于
关于![]() 的表达式,由此求出定值.
的表达式,由此求出定值.
试题解析:(I)将![]() 代入椭圆方程
代入椭圆方程![]() ,得
,得![]() ,
,
∵直线![]() 与椭圆有公共点,∴
与椭圆有公共点,∴![]() ,得
,得![]() ,
,
∴![]() .………………3分
.………………3分
又由椭圆定义知![]() ,故当
,故当![]() 时,
时,![]() 取得最小值,
取得最小值,
此时椭圆![]() 的方程为
的方程为![]() .………………4分
.………………4分
(II)设![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,
,
∴![]() .………………6分
.………………6分
同理可得![]() .………………7分
.………………7分
∴![]() ,………………9分
,………………9分
又![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴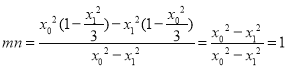 ,则
,则![]() 为定值1.………………12分
为定值1.………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合Z={(x,y)|x∈[0,2],y∈[-1,1]}.
(1)若x,y∈Z,求x+y≥0的概率;
(2)若x,y∈R,求x+y≥0的概率.
-
科目: 来源: 题型:
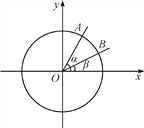
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
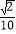 ,
,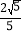 .求:
.求:(1)tan(α+β)的值;
(2)α+2β的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
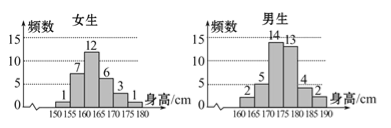
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题P;实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足x2-5x+6≤0
(1)若a=1,且
 为真命题,求实数x的取值范围。
为真命题,求实数x的取值范围。(2)若p是q成立的必要不充分条件,求实数a 的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
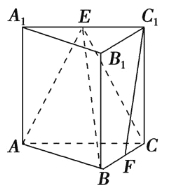
(1)求证:AB⊥平面B1BCC1; 平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
相关试题

