【题目】已知等差数列{an}中,a2=5,S5=40.等比数列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通项公式
(2)令cn=anbn,求数列{cn}的前n项和Tn.
参考答案:
【答案】(1)an=3n﹣1;(2)![]() ;(3)
;(3)![]()
【解析】试题分析:(1)设出数列的公差,分别根据等差数列的通项公式表示出![]() 和
和![]() 联立方程求得和
联立方程求得和![]() 和
和![]() ,则数列的通项公式可得,求出首项与公比,即可得
,则数列的通项公式可得,求出首项与公比,即可得![]() 的通项公式;(2)由(1)得的
的通项公式;(2)由(1)得的![]() 代入
代入![]() ,利用错位相减求和即可.
,利用错位相减求和即可.
试题解析:(1)设公差为d,则由a2=5,S5=40,得:![]() ,解得
,解得![]() ,则an=3n﹣1…
,则an=3n﹣1…
∵![]() ∴q=3
∴q=3![]() …
…
(2)![]() ①
①
∴![]() ②
②
①﹣②:![]()
∴![]() …
…
【 方法点睛】本题主要考查等比数列和等差数列的通项以及错位相减法求数列的的前![]() 项和,属于中档题.一般地,如果数列
项和,属于中档题.一般地,如果数列![]() 是等差数列,
是等差数列,![]() 是等比数列,求数列
是等比数列,求数列![]() 的前
的前![]() 项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列
项和时,可采用“错位相减法”求和,一般是和式两边同乘以等比数列![]() 的公比,然后作差求解, 在写出“
的公比,然后作差求解, 在写出“![]() ”
”![]() 与“
与“![]() ” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“
” 的表达式时应特别注意将两式“错项对齐”以便下一步准确写出“![]() ”的表达式.
”的表达式.
-
科目: 来源: 题型:
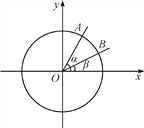
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
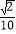 ,
,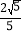 .求:
.求:(1)tan(α+β)的值;
(2)α+2β的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解学生身高情况,某校以10%的比例对全校700名学生按性别进行分层抽样调查,测得身高情况的统计图如下:
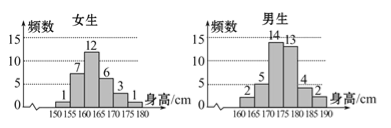
(1)估计该校男生的人数;
(2)估计该校学生身高在170~185cm之间的概率;
(3)从样本中身高在180~190cm之间的男生中任选2人,求至少有1人身高在185~190cm之间的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
 是直线
是直线 与椭圆
与椭圆 的一个公共点,
的一个公共点, 分别为该椭圆的左右焦点,设
分别为该椭圆的左右焦点,设 取得最小值时椭圆为
取得最小值时椭圆为 .
.(I)求椭圆
 的方程;
的方程;(II)已知
 是椭圆
是椭圆 上关于
上关于 轴对称的两点,
轴对称的两点, 是椭圆
是椭圆 上异于
上异于 的任意一点,直线
的任意一点,直线 分别与
分别与 轴交于点
轴交于点 ,试判断
,试判断 是否为定值,并说明理由.
是否为定值,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设命题P;实数x满足x2-4ax+3a2<0,其中a>0;命题q:实数x满足x2-5x+6≤0
(1)若a=1,且
 为真命题,求实数x的取值范围。
为真命题,求实数x的取值范围。(2)若p是q成立的必要不充分条件,求实数a 的取值范围
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.
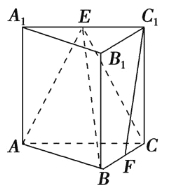
(1)求证:AB⊥平面B1BCC1; 平面ABE⊥平面B1BCC1;
(2)求证:C1F∥平面ABE;
(3)求三棱锥E-ABC的体积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班倡议假期每位学生至少阅读一本名著,为了解学生的阅读情况,对该班所有学生进行了调查.调查结果如下表:

(1)试根据上述数据,求这个班级女生阅读名著的平均本数;
(2)若从阅读5本名著的学生中任选2人交流读书心得,求选到男生和女生各1人的概率;
(3)试比较该班男生阅读名著本数的方差
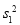 与女生阅读名著本数的方差
与女生阅读名著本数的方差 的大小(只需写出结论).
的大小(只需写出结论).
相关试题

