【题目】选修4-1《几何证明选讲》
已知A、B、C、D为圆O上的四点,直线DE为圆O的切线,AC∥DE,AC与BD相交于H点

(1)求证:BD平分∠ABC;
(2)若AB=4,AD=6,BD=8,求AH的长.
参考答案:
【答案】(1) 详见解析(2)3
【解析】
试题分析:(1)证明BD平分∠ABC实质就是求角相等:由弦切角定理得CDE=DBC ,由平行得CDE=DCA ,由同弧对等角得DBA=DCA ,三者结合得DBA=DBC (2)求线段长,一般利用相似三角形得比例关系:由ABH∽DBC,得![]() ,而由等角转化为等弦:由DBA=DBC 得AD=DC,
,而由等角转化为等弦:由DBA=DBC 得AD=DC,![]() ,解得AH=3
,解得AH=3
试题解析:证明:(1)∵AC∥DE,∴CDE=DCA,又∵DBA=DCA,∴CDE=DBA
∵直线DE为圆O的切线,∴CDE=DBC
故DBA=DBC,即BD平分∠ABC
(2)∵CAB=CDB,且DBA=DBC,∴ABH∽DBC,∴![]()
又EDC=DAC=DCA,∴AD=DC
∴![]() , ∵AB=4,AD=6,BD=8∴AH=3
, ∵AB=4,AD=6,BD=8∴AH=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】随着手机的发展,“微信”越来越成为人们交流的一种方式.某机构对“使用微信交流”的态度进行调查,随机抽取了50人,他们年龄的频数分布及对“使用微信交流”赞成人数如表:
年龄(单位:岁)
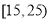
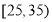
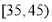
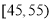
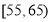
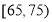
频数
5
10
15
10
5
5
赞成人数
3
10
12
7
2
1
(1)若以“年龄45岁为分界点”,由以上统计数据完成下面的
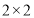 列联表,并判断是否有
列联表,并判断是否有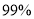 的把握认为“使用微信交流”的态度与人的年龄有关:
的把握认为“使用微信交流”的态度与人的年龄有关:年龄不低于45岁的人数
年龄低于45岁的人数
合计
赞成
不赞成
合计
(2)若从年龄在
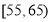 ,
,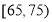 的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为
的被调查人中各随机选取两人进行追踪调查.记选中的4人中赞成“使用微信交流”的人数为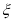 ,求随机变量
,求随机变量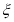 的分布列及数学期望.
的分布列及数学期望.参考数据如下:
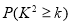
0.050
0.010
0.001
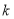
3.841
6.635
10.828
参考公式:
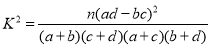 ,
,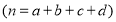 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)如图,点A,B是单位圆上的两点,A,B两点分别在第一、二象限,点C是圆与x轴正半轴的交点,△AOB是正三角形,若点A的坐标为(
 ,
, ),记∠COA=α.
),记∠COA=α.
(Ⅰ)求
 的值;
的值;(Ⅱ)求cos∠COB的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
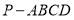 中,
中,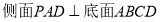 ,侧棱
,侧棱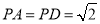 ,底面
,底面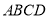 为直角梯形,其中
为直角梯形,其中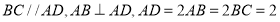 ,
,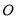 为
为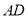 中点.
中点.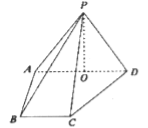
(1)求证:
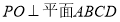 ;
;(2)求异面直线
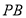 与
与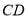 所成角的余弦值;
所成角的余弦值;(3)线段
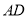 上是否存在
上是否存在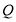 ,使得它到平面
,使得它到平面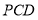 的距离为
的距离为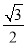 ?若存在,求出
?若存在,求出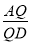 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】设p:-1≤x<2,q:x<a,若q是p的必要条件,则a的取值范围是( )
A.a≤-1B.a≤-1或a≥2C.a≥2D.-1≤a<2
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知{an}是一个公差为d(d≠0)的等差数列,它的前10项和S10=110,且a1,a2,a4成等比数列。
(1)证明:a1=d;
(2)求公差d的值和数列{an}的通项公式。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为迎接春节,某工厂大批生产小孩具—— 拼图,工厂为了规定工时定额,需要确定加工拼图所花费的时间,为此进行了10次试验,测得的数据如下:
拼图数
 /个
/个10
20
30
40
50
60
70
80
90
100
加工时间
 /分钟
/分钟62
68
75
81
89
95
102
108
115
122
(1)画出散点图,并判断
 与
与 是否具有线性相关关系;
是否具有线性相关关系;
(2)求回归方程;
(3)根据求出的回归方程,预测加工2010个拼图需要用多少小时?(精确到0.1)
附:回归直线的斜率和截距的最小二乘估计公式分别为:
 ,
,  .
.参考数据
合计

10
20
30
40
50
60
70
80
90
100
550

62
68
75
81
89
95
102
108
115
122
917

100
400
900
1600
2500
3600
4900
6400
8100
10000
38500

620
1360
2250
3240
4450
5700
7140
8840
10350
12200
55950
相关试题

