【题目】已知平面向量 ![]() =(1,x),
=(1,x), ![]() =(2x+3,﹣x)(x∈R).
=(2x+3,﹣x)(x∈R).
(1)若 ![]() ∥
∥ ![]() ,求|
,求| ![]() |
|
(2)若 ![]() 与
与 ![]() 夹角为锐角,求x的取值范围.
夹角为锐角,求x的取值范围.
(3)若| ![]() |=2,求与
|=2,求与 ![]() 垂直的单位向量
垂直的单位向量 ![]() 的坐标.
的坐标.
参考答案:
【答案】
(1)解:若 ![]() ,则﹣x﹣(2x+3)x=0,解得x=0或x=﹣2,
,则﹣x﹣(2x+3)x=0,解得x=0或x=﹣2,
当x=0时, ![]() =(﹣2,0),∴|
=(﹣2,0),∴| ![]() |=2,
|=2,
当x=﹣2时, ![]() =(2,﹣4),∴|
=(2,﹣4),∴| ![]() |=2
|=2 ![]()
(2)解:若 ![]() 与
与 ![]() 夹角为锐角,则
夹角为锐角,则 ![]() >0,即2x+3﹣x2>0,∴﹣1<x<3,
>0,即2x+3﹣x2>0,∴﹣1<x<3,
由(1)可知当x=0时, ![]() ,此时
,此时 ![]() ,
, ![]() 的夹角为0,不符合题意,舍去,
的夹角为0,不符合题意,舍去,
∴x的取值范围是(﹣1,0)∪(0,3)
(3)解:∵| ![]() |=2,∴1+x2=4,解得x=±
|=2,∴1+x2=4,解得x=± ![]() ,
,
设 ![]() =(m,n),则m+nx=0,且m2+n2=1,
=(m,n),则m+nx=0,且m2+n2=1,
∴当x= ![]() 时,
时, ![]() ,解得
,解得  或
或  ;
;
当x=﹣ ![]() 时,
时, ![]() ,解得
,解得  或
或  ,
,
所以当x= ![]() 时,
时, ![]() 的坐标为(
的坐标为( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,
, ![]() ),
),
当x=﹣ ![]() 时,
时, ![]() 的坐标为(
的坐标为( ![]() ,
, ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() )
)
【解析】(1)根据向量平面列方程解出x,求出 ![]() 的坐标即可得出|
的坐标即可得出| ![]() |;(2)令cos<
|;(2)令cos< ![]() >>0,解出x,再去掉
>>0,解出x,再去掉 ![]() 共线的情况即可;(3)根据|
共线的情况即可;(3)根据| ![]() |=2计算x,设
|=2计算x,设 ![]() =(m,n),列方程组解出即可.
=(m,n),列方程组解出即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
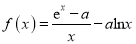 ,其中
,其中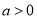 ,
, 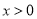 ,
, 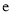 是自然对数的底数.
是自然对数的底数.(Ⅰ)讨论
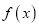 的单调性;
的单调性;(Ⅱ)设函数
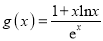 ,证明:
,证明: 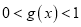 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,  ,
,  ,
,  在
在 边上,且
边上,且 ,将
,将 沿
沿 折到
折到 的位置,使得平面
的位置,使得平面 平面
平面 .
.(Ⅰ)求证:
 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
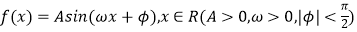 的部分图象如图所示,求:
的部分图象如图所示,求: 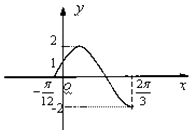
(1)f(x)的表达式.
(2)f(x)的单调增区间.
(3)f(x)的最小值以及取得最小值时的x集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
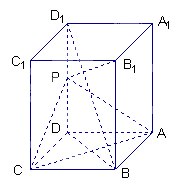
(1)求证:直线BD1∥平面PAC;
(2)求证:直线PB1⊥平面PAC.
(3)求三棱锥B﹣PAC的体积. -
科目: 来源: 题型:
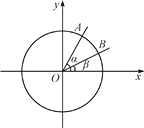
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
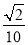 ,
, 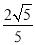 .求:
.求:(1)tan(α+β)的值;
(2)α+2β的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 :
:  ,曲线
,曲线 :
:  (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线
 ,
,  的极坐标方程;
的极坐标方程;(Ⅱ)曲线
 :
:  (
( 为参数,
为参数,  ,
,  )分别交
)分别交 ,
,  于
于 ,
,  两点,当
两点,当 取何值时,
取何值时,  取得最大值.
取得最大值.
相关试题

