【题目】函数 ![]() 的部分图象如图所示,求:
的部分图象如图所示,求: 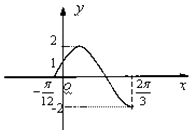
(1)f(x)的表达式.
(2)f(x)的单调增区间.
(3)f(x)的最小值以及取得最小值时的x集合.
参考答案:
【答案】
(1)解:根据函数 ![]() 的部分图象,
的部分图象,
可得A=2, ![]() =
= ![]() +
+ ![]() ,求得ω=2,∴f(x)=2sin(2x+φ).
,求得ω=2,∴f(x)=2sin(2x+φ).
再根据五点法作图可得2 ![]() +φ=
+φ= ![]() ,∴φ=
,∴φ= ![]() ,∴f(x)=2sin(2x+
,∴f(x)=2sin(2x+ ![]() )
)
(2)解:令2kπ﹣ ![]() ≤2x+
≤2x+ ![]() ≤2kπ+
≤2kπ+ ![]() ,求得kπ﹣
,求得kπ﹣ ![]() ≤x≤kπ+
≤x≤kπ+ ![]() ,
,
可得函数的增区间为[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈Z
],k∈Z
(3)解:令2x+ ![]() =2kπ﹣
=2kπ﹣ ![]() ,求得x=kπ+﹣
,求得x=kπ+﹣ ![]() ,可得当x=kπ+﹣
,可得当x=kπ+﹣ ![]() ,k∈Z 时,函数取得最小值为﹣2.
,k∈Z 时,函数取得最小值为﹣2.
即f(x)的最小值为﹣2,取得最小值时的x集合为{x|x=kπ+﹣ ![]() ,k∈Z }
,k∈Z }
【解析】(1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.(2)利用正弦函数的单调性,求得函数的增区间.(3)利用正弦函数的最值,求得f(x)的最小值以及取得最小值时的x集合.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:mx+8y+n=0和l2:2x+my﹣1=0,试确定m,n的值,使
(1)l1与l2相交于点P(m,﹣1);
(2)l1∥l2;
(3)l1⊥l2 , 且l1在y轴上的截距为﹣1. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
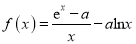 ,其中
,其中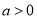 ,
, 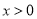 ,
, 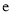 是自然对数的底数.
是自然对数的底数.(Ⅰ)讨论
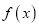 的单调性;
的单调性;(Ⅱ)设函数
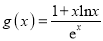 ,证明:
,证明: 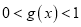 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,  ,
,  ,
,  在
在 边上,且
边上,且 ,将
,将 沿
沿 折到
折到 的位置,使得平面
的位置,使得平面 平面
平面 .
.(Ⅰ)求证:
 ;
;(Ⅱ)求二面角
 的余弦值.
的余弦值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面向量
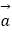 =(1,x),
=(1,x), 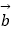 =(2x+3,﹣x)(x∈R).
=(2x+3,﹣x)(x∈R).
(1)若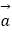 ∥
∥ 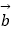 ,求|
,求|  |
|
(2)若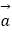 与
与 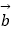 夹角为锐角,求x的取值范围.
夹角为锐角,求x的取值范围.
(3)若|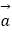 |=2,求与
|=2,求与 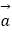 垂直的单位向量
垂直的单位向量 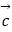 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
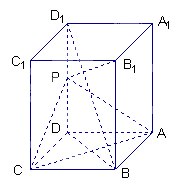
(1)求证:直线BD1∥平面PAC;
(2)求证:直线PB1⊥平面PAC.
(3)求三棱锥B﹣PAC的体积. -
科目: 来源: 题型:
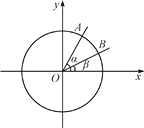
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为
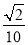 ,
, 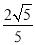 .求:
.求:(1)tan(α+β)的值;
(2)α+2β的大小.
相关试题

