【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() :
: ![]() ,曲线
,曲线![]() :
: ![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,
为极点, ![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(Ⅰ)求曲线![]() ,
, ![]() 的极坐标方程;
的极坐标方程;
(Ⅱ)曲线![]() :
: ![]() (
(![]() 为参数,
为参数, ![]() ,
, ![]() )分别交
)分别交![]() ,
, ![]() 于
于![]() ,
, ![]() 两点,当
两点,当![]() 取何值时,
取何值时, ![]() 取得最大值.
取得最大值.
参考答案:
【答案】(Ⅰ)![]() :
:![]() ,
, ![]() :
: ![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(1)利用![]() ,
, ![]() ,将直线直角坐标方程化为极坐标方程
,将直线直角坐标方程化为极坐标方程![]() ,先根据
,先根据![]() 将曲线
将曲线![]() 参数方程化为直角坐标方程
参数方程化为直角坐标方程![]() ,,再利用将曲线
,,再利用将曲线![]() 直角坐标方程化为极坐标方程
直角坐标方程化为极坐标方程![]() .(2)先确定曲线
.(2)先确定曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ,
, ![]() ),再代入曲线
),再代入曲线![]() ,
, ![]() 的极坐标方程得
的极坐标方程得![]() ,从而理二倍角公式及配角公式化简
,从而理二倍角公式及配角公式化简![]() 得
得![]() ,最后根据正弦函数性质求最值.
,最后根据正弦函数性质求最值.
试题解析:(Ⅰ)因为![]() ,
, ![]() ,
, ![]() ,
,
![]() 的极坐标方程为
的极坐标方程为![]() ,
,
![]() 的普通方程为
的普通方程为![]() ,即
,即![]() ,对应极坐标方程为
,对应极坐标方程为![]() .
.
(Ⅱ)曲线![]() 的极坐标方程为
的极坐标方程为![]() (
(![]() ,
, ![]() )
)
设![]() ,
, ![]() ,则
,则![]() ,
, ![]() ,
,
所以![]()
![]()
![]()
![]() ,
,
又![]() ,
, ![]() ,
,
所以当![]() ,即
,即![]() 时,
时, ![]() 取得最大值
取得最大值![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A1,∠A2,…,∠An为凸多边形的内角,且lg sin A1+lg sin A2+…+lg sin An=0,则这个多边形是( )
A. 正六边形 B. 梯形
C. 矩形 D. 含锐角的菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A,B,C的坐标分别为A(3,0),B(0,3),C(cos α,sin α),α∈
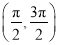 .
.(1)若|
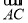 |=|
|=|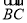 |,求角α的值;
|,求角α的值;(2)若
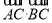 =-1,求
=-1,求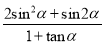 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若奇函数y=f(x)在区间(0,+∞)上是增函数,又f(﹣3)=0,则不等式f(x)<0的解集为( )
A.(﹣3,0)∪(3,+∞)
B.(﹣3,0)∪(0,3)
C.(﹣∞,﹣3)∪(0,3)
D.(﹣∞,﹣3)∪(3,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
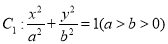 ()的焦距为4,左、右焦点分别为
()的焦距为4,左、右焦点分别为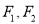 ,且
,且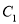 与抛物线
与抛物线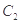 :
: 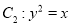
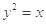 的交点所在的直线经过
的交点所在的直线经过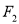 .
.(Ⅰ)求椭圆
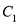 的方程;
的方程;(Ⅱ)过
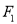
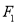 的直线
的直线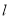
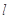 与
与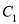 交于
交于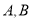 两点,与抛物线
两点,与抛物线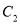 无公共点,求
无公共点,求 的面积的取值范围.
的面积的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某保险公司有一款保险产品的历史收益率(收益率=利润÷保费收入)的频率分布直方图如图所示:

(Ⅰ)试估计平均收益率;
(Ⅱ)根据经验,若每份保单的保费在20元的基础上每增加
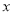 元,对应的销量
元,对应的销量 (万份)与
(万份)与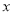 (元)有较强线性相关关系,从历史销售记录中抽样得到如下5组
(元)有较强线性相关关系,从历史销售记录中抽样得到如下5组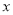 与
与 的对应数据:
的对应数据:
据此计算出的回归方程为
 .
.(i)求参数
 的估计值;
的估计值;(ii)若把回归方程
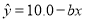 当作
当作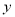 与
与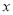 的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益.
的线性关系,用(Ⅰ)中求出的平均收益率估计此产品的收益率,每份保单的保费定为多少元时此产品可获得最大收益,并求出该最大收益. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:mx+8y+n=0和l2:2x+my﹣1=0,试确定m,n的值,使
(1)l1与l2相交于点P(m,﹣1);
(2)l1∥l2;
(3)l1⊥l2 , 且l1在y轴上的截距为﹣1.
相关试题

