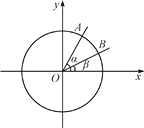
【题目】如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α,β,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为![]() ,
, ![]() .求:
.求:
(1)tan(α+β)的值;
(2)α+2β的大小.
参考答案:
【答案】(1)-3;(2) α+2β=![]() .
.
【解析】试题分析:(1)根据题意,由三角函数的定义可得![]() 与
与![]() 的值,进而可得出
的值,进而可得出![]() 与
与![]() 的值,从而可求
的值,从而可求![]() 与
与![]() 的值就,结合两角和正切公式可得答案;(2)由两角和的正切公式,可得出
的值就,结合两角和正切公式可得答案;(2)由两角和的正切公式,可得出![]() 的值,再根据
的值,再根据![]() 的取值范围,可得出
的取值范围,可得出![]() 的取值范围,进而可得出
的取值范围,进而可得出![]() 的值.
的值.
试题解析:15.解:(1)∵![]() ,从而
,从而![]() .
.
又∵![]() ,∴
,∴![]() . …
. …
利用同角三角函数的基本关系可得sin2(α﹣β)+cos2(α﹣β)=1,且![]() ,
,
解得 由条件得cosα=![]() ,cosβ=
,cosβ=![]() .
.
∵ α,β为锐角,
∴ sinα=![]() =
=![]() ,sinβ=
,sinβ=![]() =
=![]() .
.
因此tanα=![]() =7,tanβ=
=7,tanβ=![]() =
=![]() .
.
(1) tan(α+β)=![]() =
=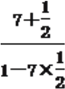 =-3.
=-3.
(2) ∵ tan2β=![]() =
=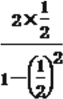 =
=![]() ,
,
∴ tan(α+2β)=![]() =
=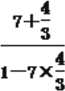 =-1.
=-1.
∵ α,β为锐角,∴ 0<α+2β<![]() ,∴ α+2β=
,∴ α+2β=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数
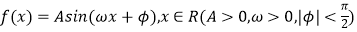 的部分图象如图所示,求:
的部分图象如图所示,求: 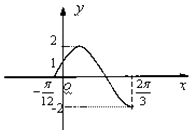
(1)f(x)的表达式.
(2)f(x)的单调增区间.
(3)f(x)的最小值以及取得最小值时的x集合. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知平面向量
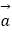 =(1,x),
=(1,x), 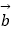 =(2x+3,﹣x)(x∈R).
=(2x+3,﹣x)(x∈R).
(1)若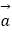 ∥
∥ 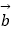 ,求|
,求|  |
|
(2)若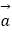 与
与 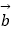 夹角为锐角,求x的取值范围.
夹角为锐角,求x的取值范围.
(3)若|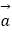 |=2,求与
|=2,求与 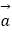 垂直的单位向量
垂直的单位向量 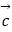 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
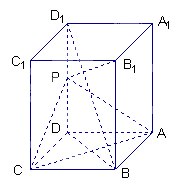
(1)求证:直线BD1∥平面PAC;
(2)求证:直线PB1⊥平面PAC.
(3)求三棱锥B﹣PAC的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】选修4-4:坐标系与参数方程
在平面直角坐标系
 中,曲线
中,曲线 :
:  ,曲线
,曲线 :
:  (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点,  轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.(Ⅰ)求曲线
 ,
,  的极坐标方程;
的极坐标方程;(Ⅱ)曲线
 :
:  (
( 为参数,
为参数,  ,
,  )分别交
)分别交 ,
,  于
于 ,
,  两点,当
两点,当 取何值时,
取何值时,  取得最大值.
取得最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某保险公司针对企业职工推出一款意外险产品,每年每人只要交少量保费,发生意外后可一次性获赔50万元.保险公司把职工从事的所有岗位共分为
 、
、 、
、 三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).
三类工种,根据历史数据统计出三类工种的每赔付频率如下表(并以此估计赔付概率).

(Ⅰ)根据规定,该产品各工种保单的期望利润都不得超过保费的20%,试分别确定各类工种每张保单保费的上限;
(Ⅱ)某企业共有职工20000人,从事三类工种的人数分布比例如图,老板准备为全体职工每人购买一份此种保险,并以(Ⅰ)中计算的各类保险上限购买,试估计保险公司在这宗交易中的期望利润.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
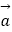 =(sin
=(sin 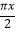 ,sin
,sin  ),
), 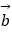 =(cos
=(cos 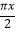 ,cos
,cos  ),且向量
),且向量 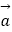 与向量
与向量 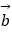 共线.
共线.
(1)求证:sin(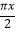 ﹣
﹣  )=0;
)=0;
(2)若记函数f(x)=sin(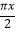 ﹣
﹣  ),求函数f(x)的对称轴方程;
),求函数f(x)的对称轴方程;
(3)求f(1)+f(2)+f(3)+…+f(2013)的值;
(4)如果已知角0<A<B<π,且A+B+C=π,满足f(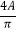 )=f(
)=f( 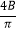 )=
)=  ,求
,求 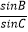 的值.
的值.
相关试题

