【题目】为了对某课题进行研究,用分层抽样方法从三所高校![]() 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
高校 | 相关人数 | 抽取人数 |
A | 18 |
|
B | 36 | 2 |
C | 54 |
|
(Ⅰ)求![]() ,
,![]() ;
;
(Ⅱ)若从高校![]() 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校![]() 的概率.
的概率.
参考答案:
【答案】(Ⅰ)![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】试题分析:(Ⅰ)利用分层抽样的特点(等比例抽样)进行求解;(Ⅱ)利用列举法得到所有和符合题意的基本事件和基本事件个数,再利用古典概型的概率公式进行求解.
试题解析:(Ⅰ)由题意可得![]() ,∴
,∴![]() ,
,![]() .
.
(Ⅱ)记从高校![]() 抽取的2人为
抽取的2人为![]() ,从高校
,从高校![]() 抽取的3人为
抽取的3人为![]() ,则从高校
,则从高校![]() 抽取的5人中选2人作专题发言的基本事件有
抽取的5人中选2人作专题发言的基本事件有![]() ,共10种.
,共10种.
设选中的2人都来自高校![]() 的事件为
的事件为![]() ,则
,则![]() 包含的基本事件有
包含的基本事件有![]() ,共3种,
,共3种,
因此![]() ,故选中的2人都来自高校
,故选中的2人都来自高校![]() 的概率为
的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“开门大吉”是某电视台推出的游戏益智节目.选手面对
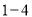 号
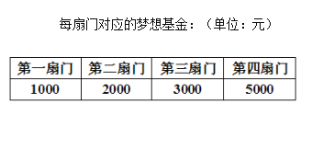
号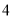 扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段:
扇大门,依次按响门上的门铃,门铃会播放一段音乐(将一首经典流行歌曲以单音色旋律的方式演绎),选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金.正确回答每一扇门后,选手可自由选择带着奖金离开比赛,还可继续挑战后面的门以获得更多奖金.(奖金金额累加)但是一旦回答错误,奖金将清零,选手也会离开比赛.在一次场外调查中,发现参加比赛的选手多数分为两个年龄段: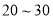 ;
;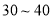 (单位:岁),其猜对歌曲名称与否人数如图所示.
(单位:岁),其猜对歌曲名称与否人数如图所示.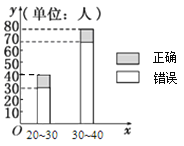
(1)写出
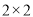 列联表:判断是否有
列联表:判断是否有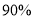 的把握认为猜对歌曲名称与否与年龄有关?
的把握认为猜对歌曲名称与否与年龄有关?说明你的理由.(下面的临界值表供参考)

(2)若某选手能正确回答第一、二、三、四扇门的概率分别为
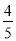 ,
,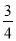 ,
,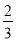 ,
,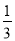 ,正确回答一个问题后,选择继续回答下一个问题的概率是
,正确回答一个问题后,选择继续回答下一个问题的概率是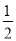 ,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为
,且各个问题回答正确与否互不影响.设该选手所获梦想基金总数为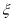 ,求
,求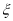 的分布列及数学期望.
的分布列及数学期望.(参考公式
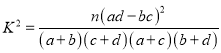 其中
其中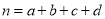 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
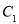 :
: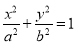 (
(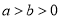 )的离心率为
)的离心率为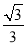 ,连接椭圆的四个顶点得到的四边形的面积为
,连接椭圆的四个顶点得到的四边形的面积为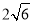 .
.(1)求椭圆
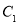 的方程;
的方程;(2)设椭圆
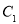 的左焦点为
的左焦点为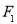 ,右焦点为
,右焦点为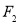 ,直线
,直线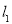 过点
过点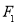 且垂直于椭圆的长轴,动直线
且垂直于椭圆的长轴,动直线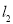 垂直
垂直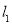 于点
于点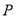 ,线段
,线段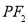 的垂直平分线交
的垂直平分线交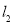 于点
于点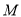 ,求点
,求点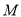 的轨迹
的轨迹 的方程;
的方程;(3)设
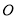 为坐标原点,取
为坐标原点,取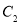 上不同于
上不同于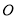 的点
的点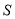 ,以
,以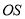 为直径作圆与
为直径作圆与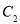 相交另外一点
相交另外一点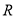 ,求该圆面积的最小值时点
,求该圆面积的最小值时点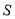 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】“珠算之父”程大为是我国明代伟大数学家,他的应用数学巨著《算法统综》的问世,标志着我国的算法由筹算到珠算转变的完成,程大位在《算法统综》中常以诗歌的形式呈现数学问题,其中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节三升九,上稍四节储三升,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明”(【注】三升九:3.9升,次第盛;盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节的容积为( )
A.
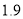 升 B.
升 B. 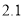 升 C.
升 C.  升 D.
升 D. 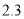 升
升 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
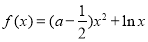 ,
,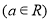 .
.(1)当
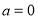 时,求
时,求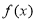 在区间
在区间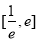 上的最大值;
上的最大值;(2)若在区间
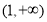 上,函数
上,函数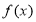 的图象恒在直线
的图象恒在直线 下方,求
下方,求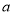 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:
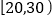 ,
,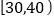 ,…,
,…,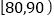 ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间
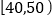 内的人数;
内的人数;(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义
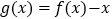 的零点
的零点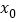 为
为 的不动点,已知函数
的不动点,已知函数 .
.Ⅰ.当
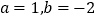 时,求函数
时,求函数 的不动点;
的不动点;Ⅱ.对于任意实数
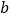 ,函数
,函数 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数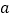 的取值范围;
的取值范围;Ⅲ.若函数
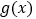 只有一个零点且
只有一个零点且 ,求实数
,求实数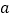 的最小值.
的最小值.
相关试题

