【题目】定义![]() 的零点
的零点![]() 为
为![]() 的不动点,已知函数
的不动点,已知函数![]() .
.
Ⅰ.当![]() 时,求函数
时,求函数![]() 的不动点;
的不动点;
Ⅱ.对于任意实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数![]() 的取值范围;
的取值范围;
Ⅲ.若函数![]() 只有一个零点且
只有一个零点且![]() ,求实数
,求实数![]() 的最小值.
的最小值.
参考答案:
【答案】(1) ![]() 的不动点为3,-1;(2)
的不动点为3,-1;(2) ![]() ;(3)
;(3) ![]() 的最小值为1.
的最小值为1.
【解析】试题分析: (1)将![]() 代入函数
代入函数![]() 的表达式,根据零点概念求出方程的根;(2)把函数
的表达式,根据零点概念求出方程的根;(2)把函数![]() 恒有两个相异的不动点,转化为对于任意实数
恒有两个相异的不动点,转化为对于任意实数![]() ,
,![]() 恒有两个不等的实数根问题,
恒有两个不等的实数根问题,![]() 即
即![]() 对任意实数
对任意实数![]() 都成立,求出b的范围即可;(3) 函数
都成立,求出b的范围即可;(3) 函数![]() 只有一个零点,则
只有一个零点,则![]() ,利用分离参数法得出
,利用分离参数法得出![]() ,根据基本不等式求出最值.
,根据基本不等式求出最值.
试题解析:(1)![]() ,
,
![]() ,
,
![]() 或-1.
或-1.
故函数![]() 的不动点为3,-1.
的不动点为3,-1.
(2) 对于任意实数![]() ,函数
,函数![]() 恒有两个相异的不动点,
恒有两个相异的不动点,
则对于任意实数![]() ,
,![]() 恒有两个不等的实数根.
恒有两个不等的实数根.
所以![]() ,
,![]() 恒成立,
恒成立,
所以![]() ,
,
所以![]() 对任意实数
对任意实数![]() 都成立,
都成立,
所以![]() ,
,
所以![]() .
.
(3)![]() ,函数
,函数![]() 只有一个零点,
只有一个零点,![]() ,
,
则![]() ,
,
所以![]() ,
,
所以![]()
![]() .
.
当且仅当![]() 时等号成立,
时等号成立,
所以![]() ,
,![]() 的最小值为1.
的最小值为1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了对某课题进行研究,用分层抽样方法从三所高校
 的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)
的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人)高校
相关人数
抽取人数
A
18
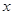
B
36
2
C
54
(Ⅰ)求
 ,
,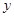 ;
;(Ⅱ)若从高校
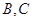 抽取的人中选2人作专题发言,求这二人都来自高校
抽取的人中选2人作专题发言,求这二人都来自高校 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
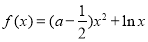 ,
,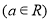 .
.(1)当
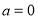 时,求
时,求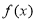 在区间
在区间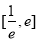 上的最大值;
上的最大值;(2)若在区间
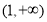 上,函数
上,函数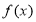 的图象恒在直线
的图象恒在直线 下方,求
下方,求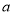 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某大学艺术专业400名学生参加某次测评,根据男女学生人数比例,使用分层抽样的方法从中随机抽取了100名学生,记录他们的分数,将数据分成7组:
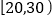 ,
,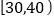 ,…,
,…,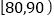 ,并整理得到如下频率分布直方图:
,并整理得到如下频率分布直方图:
(1)从总体的400名学生中随机抽取一人,估计其分数小于70的概率;
(2)已知样本中分数小于40的学生有5人,试估计总体中分数在区间
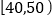 内的人数;
内的人数;(3)已知样本中有一半男生的分数不小于70,且样本中分数不小于70的男女生人数相等,试估计总体中男生和女生人数的比例.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的
 列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽1人为优秀的概率为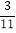 .
.优秀
非优秀
合计
甲班
10
乙班
30
合计
110
Ⅰ.请完成上面的列联表;
Ⅱ.根据列联表的数据,是否有
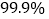 的把握认为“成绩与班级有关系”.
的把握认为“成绩与班级有关系”.参考公式与临界值表:
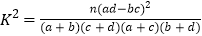 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系
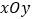 中,曲线
中,曲线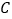 :
: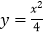 与直线
与直线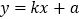 (
( )交于
)交于 ,
,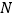 两点.
两点.(1)当
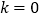 时,分别求
时,分别求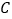 在点
在点 和
和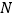 处的切线方程;
处的切线方程;(2)
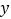 轴上是否存在点
轴上是否存在点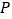 ,使得当
,使得当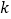 变动时,总有
变动时,总有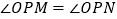 ?说明理由.
?说明理由.
相关试题

