【题目】已知点![]() 是椭圆
是椭圆![]() 的左右顶点,点
的左右顶点,点![]() 是椭圆的上顶点,若该椭圆的焦距为
是椭圆的上顶点,若该椭圆的焦距为![]() ,直线
,直线![]() ,
,![]() 的斜率之积为
的斜率之积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() ,使得以
,使得以![]() 为直径的圆经过点
为直径的圆经过点![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
参考答案:
【答案】(1)![]() . (2)存在;直线
. (2)存在;直线![]() 的方程为:
的方程为:![]() 或
或![]() .
.
【解析】试题分析:(1)由题意得![]() ,联立
,联立![]() ,解得椭圆方程(2) 设直线
,解得椭圆方程(2) 设直线![]() 的方程为
的方程为![]() ,联立椭圆方程,由根与系数之间关系求得
,联立椭圆方程,由根与系数之间关系求得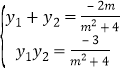 ,代入整理求得答案
,代入整理求得答案
解析:(1)由题意可知,![]() ,
,![]() ,
,
有 ![]() ,
,
即![]() ,又
,又![]() ,
,
解得![]() ,所以椭圆
,所以椭圆![]() 的方程为
的方程为![]() .
.
(2)存在;
以![]() 为直径的圆经过点
为直径的圆经过点![]() 可得,
可得,![]() ,若直线
,若直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 为点
为点![]() ,此时
,此时![]() ,此时
,此时![]() 不垂直,不满足题意,可设直线
不垂直,不满足题意,可设直线![]() 的方程为:
的方程为:![]() ,联立
,联立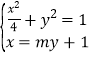 ,消
,消![]() 可得,
可得,![]() ,
,
则有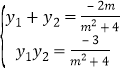 . ①
. ①
设![]() ,由题意可知
,由题意可知![]() ,因为
,因为![]() ,
,
则![]() ,即
,即![]() ,
,
整理可得:![]() , ②
, ②
将①代入②可得:![]() ,
,
整理得![]() ,解得
,解得![]() 或者
或者![]() ,
,
所以直线![]() 的方程为:
的方程为:![]() 或
或![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 过点
过点 ,其参数方程为
,其参数方程为 (
( 为参数,
为参数, ),以
),以 为极点,
为极点, 轴非负半轴为极轴建立极坐标系,曲线
轴非负半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求曲线
 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)求已知曲线
 和曲线
和曲线 交于
交于 两点,且
两点,且 ,求实数
,求实数 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某食品集团生产的火腿按行业生产标准分成8个等级,等级系数
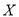 依次为1,2,3,…,8,其中
依次为1,2,3,…,8,其中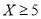 为标准
为标准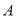 ,
, 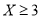 为标准
为标准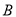 .已知甲车间执行标准
.已知甲车间执行标准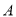 ,乙车间执行标准
,乙车间执行标准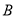 生产该产品,且两个车间的产品都符合相应的执行标准.
生产该产品,且两个车间的产品都符合相应的执行标准.(1)已知甲车间的等级系数
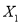 的概率分布列如下表,若
的概率分布列如下表,若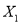 的数学期望E(X1)=6.4,求
的数学期望E(X1)=6.4,求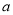 ,
, 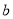 的值;
的值;X1
5
6
7
8
P
0.2
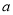
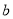
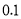
(2)为了分析乙车间的等级系数
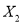 ,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7
,从该车间生产的火腿中随机抽取30根,相应的等级系数组成一个样本如下:3 5 3 3 8 5 5 6 3 4 6 3 4 7 5 3 4 8 5 3 8 3 4 3 4 4 7 5 6 7用该样本的频率分布估计总体,将频率视为概率,求等级系数
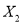 的概率分布列和均值;
的概率分布列和均值;(3)从乙车间中随机抽取5根火腿,利用(2)的结果推断恰好有三根火腿能达到标准
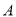 的概率.
的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
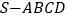 ,
,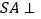 平面
平面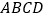 ,底面
,底面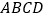 为直角梯形,
为直角梯形,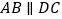 ,
,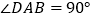 ,
,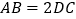 ,
,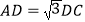 ,
,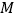 是
是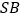 中点.
中点.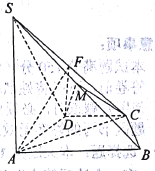
(1)求证:
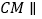 平面
平面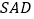 ;
;(2)若直线
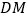 与平面
与平面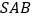 所成角的正切值为
所成角的正切值为 ,
,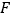 是
是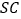 的中点,求二面角
的中点,求二面角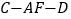 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
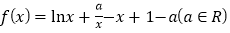 .
.(1)求函数
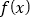 的单调区间;
的单调区间;(2)若存在
 ,使
,使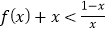 成立,求整数
成立,求整数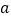 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:
 )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:数据分组







频数
3
8
9
12
10
5
3
(1)根据频数分布表,求该产品尺寸落在
 的概率;
的概率;(2)求这50件产品尺寸的样本平均数
 .(同一组中的数据用该组区间的中点值作代表);
.(同一组中的数据用该组区间的中点值作代表);(3)根据产品的频数分布,求出产品尺寸中位数的估计值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】四棱台被过点
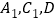 的平面截去一部分后得到如图所示的几何体,其下底面四边形
的平面截去一部分后得到如图所示的几何体,其下底面四边形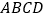 是边长为2的菱形,
是边长为2的菱形,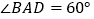 ,
,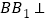 平面
平面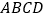 ,
,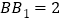 .
.(Ⅰ)求证:平面
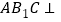 平面
平面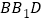 ;
;(Ⅱ)若
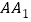 与底面
与底面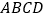 所成角的正切值为2,求二面角
所成角的正切值为2,求二面角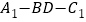 的余弦值.
的余弦值.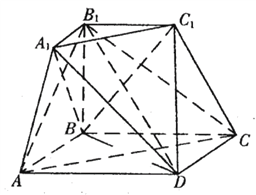
相关试题

