【题目】从某工厂的一个车间抽取某种产品50件,产品尺寸(单位:![]() )落在各个小组的频数分布如下表:
)落在各个小组的频数分布如下表:
数据分组 |
|
|
|
|
|
|
|
频数 | 3 | 8 | 9 | 12 | 10 | 5 | 3 |
(1)根据频数分布表,求该产品尺寸落在![]() 的概率;
的概率;
(2)求这50件产品尺寸的样本平均数![]() .(同一组中的数据用该组区间的中点值作代表);
.(同一组中的数据用该组区间的中点值作代表);
(3)根据产品的频数分布,求出产品尺寸中位数的估计值.
参考答案:
【答案】(1)0.16;(2)22.7;(3)22.75
【解析】试题分析:(1)根据频数分布表可知,产品尺寸落在![]() 内的个数为8,从而所求概率为
内的个数为8,从而所求概率为![]() .(2)根据“同一组中的数据用该组区间的中点值作代表”可以计算
.(2)根据“同一组中的数据用该组区间的中点值作代表”可以计算![]() 件产品的样本平均数为
件产品的样本平均数为![]() .(3)根据频数分布表可知中位数必定在区间
.(3)根据频数分布表可知中位数必定在区间![]() ,前3组的产品个数共
,前3组的产品个数共![]() 个,故中位数的估计值为
个,故中位数的估计值为![]() .
.
解析:(1)根据频数分布表可知,产品尺寸落在![]() 内的概率
内的概率![]() .
.
(2)样本平均数
![]() .
.
(3)![]() .
.![]() 中位数在区间
中位数在区间![]() 上,
上,![]() 中位数为
中位数为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
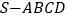 ,
,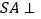 平面
平面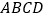 ,底面
,底面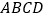 为直角梯形,
为直角梯形,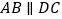 ,
,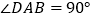 ,
,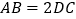 ,
,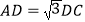 ,
,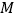 是
是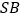 中点.
中点.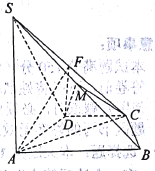
(1)求证:
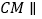 平面
平面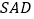 ;
;(2)若直线
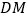 与平面
与平面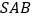 所成角的正切值为
所成角的正切值为 ,
,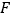 是
是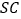 的中点,求二面角
的中点,求二面角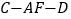 的余弦值.
的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
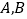 是椭圆
是椭圆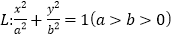 的左右顶点,点
的左右顶点,点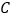 是椭圆的上顶点,若该椭圆的焦距为
是椭圆的上顶点,若该椭圆的焦距为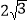 ,直线
,直线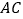 ,
,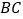 的斜率之积为
的斜率之积为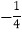 .
.(1)求椭圆
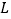 的方程;
的方程;(2)是否存在过点
 的直线
的直线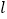 与椭圆
与椭圆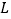 交于两点
交于两点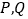 ,使得以
,使得以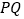 为直径的圆经过点
为直径的圆经过点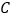 ?若存在,求出直线
?若存在,求出直线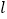 的方程,若不存在,说明理由.
的方程,若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
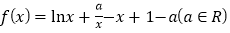 .
.(1)求函数
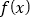 的单调区间;
的单调区间;(2)若存在
 ,使
,使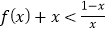 成立,求整数
成立,求整数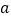 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱台被过点
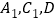 的平面截去一部分后得到如图所示的几何体,其下底面四边形
的平面截去一部分后得到如图所示的几何体,其下底面四边形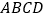 是边长为2的菱形,
是边长为2的菱形,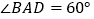 ,
,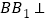 平面
平面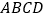 ,
,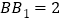 .
.(Ⅰ)求证:平面
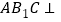 平面
平面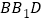 ;
;(Ⅱ)若
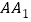 与底面
与底面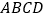 所成角的正切值为2,求二面角
所成角的正切值为2,求二面角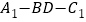 的余弦值.
的余弦值.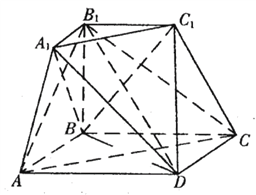
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年12月,针对国内天然气供应紧张的问题,某市政府及时安排部署,加气站采取了紧急限气措施,全市居民打响了节约能源的攻坚战.某研究人员为了了解天然气的需求状况,对该地区某些年份天然气需求量进行了统计,并绘制了相应的折线图.
(Ⅰ)由折线图可以看出,可用线性回归模型拟合年度天然气需示量
 (单位:千万立方米)与年份
(单位:千万立方米)与年份 (单位:年)之间的关系.并且已知
(单位:年)之间的关系.并且已知 关于
关于 的线性回归方程是
的线性回归方程是 ,试确定
,试确定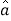 的值,并预测2018年该地区的天然气需求量;
的值,并预测2018年该地区的天然气需求量;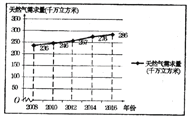
(Ⅱ)政府部门为节约能源出台了《购置新能源汽车补贴方案》,该方案对新能源汽车的续航里程做出了严格规定,根据续航里程的不同,将补贴金额划分为三类,A类:每车补贴1万元,B类:每车补贴2.5万元,C类:每车补贴3.4万元.某出租车公司对该公司60辆新能源汽车的补贴情况进行了统计,结果如下表:
类型
 类
类 类
类 类
类车辆数目
10
20
30
为了制定更合理的补贴方案,政府部门决定利用分层抽样的方式了解出租车公司新能源汽车的补贴情况,在该出租车公司的60辆车中抽取6辆车作为样本,再从6辆车中抽取2辆车进一步跟踪调查.若抽取的2辆车享受的补贴金额之和记为“
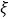 ”,求
”,求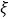 的分布列及期望.
的分布列及期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】椭圆
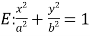 (
(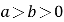 )的左、右焦点分别为
)的左、右焦点分别为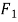 ,
,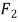 ,过
,过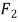 作垂直于
作垂直于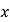 轴的直线
轴的直线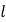 与椭圆
与椭圆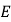 在第一象限交于点
在第一象限交于点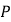 ,若
,若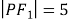 ,且
,且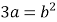 .
.(Ⅰ)求椭圆
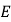 的方程;
的方程;(Ⅱ)
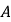 ,
,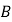 是椭圆
是椭圆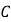 上位于直线
上位于直线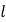 两侧的两点.若直线
两侧的两点.若直线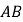 过点
过点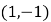 ,且
,且 ,求直线
,求直线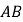 的方程.
的方程.
相关试题

