【题目】已知数集![]() 具有性质
具有性质![]() :对任意的
:对任意的![]()
![]() ,
,![]() ,使得
,使得![]() 成立.
成立.
(Ⅰ)分别判断数集![]() 与
与![]() 是否具有性质
是否具有性质![]() ,并说明理由;
,并说明理由;
(Ⅱ)求证![]() ;
;
(Ⅲ)若![]() ,求数集
,求数集![]() 中所有元素的和的最小值.
中所有元素的和的最小值.
参考答案:
【答案】(1)具有(2)见解析(3)最小值为![]()
【解析】试题分析:
(1)利用性质![]() 的含义及特例可判断数集
的含义及特例可判断数集![]() 不具有性质
不具有性质![]() ,数集
,数集![]() 具有性质
具有性质![]() .(2)数集
.(2)数集![]() 具有性质
具有性质![]() 可得
可得![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
将上述不等式相加得![]() ,化简得
,化简得![]() ,即为所求.(3)由
,即为所求.(3)由![]() 及性质
及性质![]() 可得
可得![]() ,从而易知数集
,从而易知数集![]() 的元素都是整数,构造
的元素都是整数,构造![]() 或者
或者![]() ,此时元素和为
,此时元素和为![]() ,然后再证明
,然后再证明![]() 是最小的和.
是最小的和.
试题解析:
(![]() )∵
)∵![]() ,
,
∴数集![]() 不具有性质
不具有性质![]() .
.
∵![]() ,
, ![]() ,
, ![]() ,
,
∴数集![]() 具有性质
具有性质![]() .
.
(![]() )∵集合
)∵集合![]() 具有性质
具有性质![]() 即对任意的
即对任意的![]() ,
, ![]() ,
, ![]() 使得
使得![]() 成立,
成立,
又![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
, ![]() ,
,
∴![]() ,
,
即![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
将上述不等式相加得![]() ,
,
化简得![]() .
.
(![]() )最小值为
)最小值为![]() .
.
首先注意到![]() ,根据性质
,根据性质![]() ,得到
,得到![]() ,
,
所以易知数集![]() 的元素都是整数,
的元素都是整数,
构造![]() 或者
或者![]() ,这两个集合具有性质
,这两个集合具有性质![]() ,此时元素和为
,此时元素和为![]() .
.
下面,证明![]() 是最小的和.
是最小的和.
假设数集![]() ,满足
,满足![]() 最小(存在性显然,因为满足
最小(存在性显然,因为满足![]() 的数集
的数集![]() 只有有限个).
只有有限个).
第一步:首先说明集合![]() 中至少有
中至少有![]() 个元素:
个元素:
由(![]() )可知,
)可知, ![]() ,
, ![]() ,
, ![]() ,
,
又![]() ,
,
∴![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
∴![]() .
.
第二步:证明![]() ,
, ![]() ,
, ![]() ,
,
若![]() ,设
,设![]() ,
,
∵![]() ,为了使
,为了使![]() 最小,
最小,
在集合![]() 中一定不含有元素
中一定不含有元素![]() ,使得
,使得![]() ,
,
从而![]() ;
;
若![]() ,根据性质
,根据性质![]() ,对
,对![]() ,有
,有![]() ,
, ![]() ,使得
,使得![]() ,
,
显然![]() ,
,
∴![]() ,
,
此时集合![]() 中至少有
中至少有![]() 个不同于
个不同于![]() ,
, ![]() ,
, ![]() 的元素,
的元素,
从而![]() ,矛盾,
,矛盾,
∴![]() ,进而,
,进而, ![]() ,且
,且![]() .
.
同理可证:若![]() ,则
,则![]() .
.
假设![]() ,
,
∵![]() ,根据性质
,根据性质![]() ,有
,有![]() ,
, ![]() ,使得
,使得![]() ,
,
显然![]() ,
,
∴![]() ,
,
此时集合![]() 中至少还有
中至少还有![]() 个不同于
个不同于![]() ,
, ![]() ,
, ![]() ,
, ![]() 的元素,
的元素,
从而![]() ,矛盾,
,矛盾,
∴![]() ,且
,且![]() ,
,
同理可证:若![]() ,则
,则![]() .
.
假设![]() ,
,
∵![]() ,根据性质
,根据性质![]() ,有
,有![]() ,
, ![]() ,使得
,使得![]() ,
,
显然![]() ,
,
∴![]() ,
,
此时集合![]() 中至少还有
中至少还有![]() 个不同于
个不同于![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的元素,
的元素,
从而![]() ,矛盾,
,矛盾,
∴![]() ,且
,且![]() .
.
至此,我们得到![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
根据性质![]() ,有
,有![]() ,
, ![]() ,使得
,使得![]() ,我们需要考虑如下几种情形:
,我们需要考虑如下几种情形:
①![]() ,
, ![]() ,此时集合中至少还需要一个大于等于
,此时集合中至少还需要一个大于等于![]() 的元素
的元素![]() ,才能得到元素
,才能得到元素![]() ,则
,则![]() ;
;
②![]() ,
, ![]() ,此时集合中至少还需要一个大于
,此时集合中至少还需要一个大于![]() 的元素
的元素![]() ,才能得到元素
,才能得到元素![]() ,则
,则![]() ;
;
③![]() ,
, ![]() ,此时集合
,此时集合![]() ,
, ![]() ;
;
④![]() ,
, ![]() ,此时集合
,此时集合![]() ,
, ![]() .
.
综上所述,若![]() ,则数集
,则数集![]() 中所有元素的和的最小值是
中所有元素的和的最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足:
满足:  ,
,  .
.(
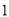 )求
)求 ,
,  ,
,  的值.
的值.(
 )求证:数列
)求证:数列 是等比数列.
是等比数列.(
 )令
)令 ,如果对任意
,如果对任意 ,都有
,都有 ,求实数
,求实数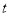 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b , g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a , b , c , d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】36的所有正约数之和可按如下方法得到:因为36=22×32 , 所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可得100的所有正约数之和为( )
A.217
B.273
C.455
D.651 -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:
①函数
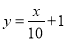 的图象与
的图象与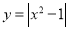 的图象恰有
的图象恰有 个公共点;
个公共点;②函数
 有
有 个零点;
个零点;③若函数
 与
与 的图像关于直线
的图像关于直线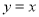 对称,则函数
对称,则函数 与
与 的图象也关于直线
的图象也关于直线 对称;
对称;④函数
 的图象是由函数
的图象是由函数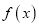 的图象水平向右平移一个单位后,将所得图象在
的图象水平向右平移一个单位后,将所得图象在 轴右侧部分沿
轴右侧部分沿 轴翻折到
轴翻折到 轴左侧替代
轴左侧替代 轴左侧部分图象,并保留右侧部分而得到的.其中错误的命题有___________.(填写所有错误的命题的序号)
轴左侧部分图象,并保留右侧部分而得到的.其中错误的命题有___________.(填写所有错误的命题的序号) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
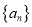 满足
满足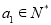 ,且
,且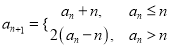 .
.(1)当
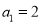 时,写出
时,写出 的通项公式(直接写出答案,无需过程);
的通项公式(直接写出答案,无需过程);(2)求最小整数
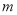 ,使得当
,使得当 时,
时, 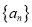 是单调递增数列;
是单调递增数列;(3)是否存在
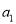 使得
使得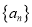 是等比数列?若存在请求出;若不存在请说明理由.
是等比数列?若存在请求出;若不存在请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆C:(x-3)2+(y-4)2=1,设点P是圆C上的动点.记d=|PB|2+|PA|2,其中A(0,1),B(0,-1),则d的取值范围为________.
相关试题

