【题目】已知函数f(x)=x2+ax+b , g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a , b , c , d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围.
参考答案:
【答案】
(1)解:根据题意![]() ,因为f
,因为f![]() (x)=2x+a,g
(x)=2x+a,g![]() (x)=ex(cx+2)+c
(x)=ex(cx+2)+c![]() ex,则由导数的几何意义可知
ex,则由导数的几何意义可知![]() ,所以
,所以 ![]() =2.
=2.
(2)解:由(1)知, ![]() ,
,
设函数 ![]() ,
,
![]() .
.
由题设可得 ![]() ,即
,即 ![]() ,
,
令 ![]() 得
得 ![]()
①若 ![]() ,则
,则 ![]() ,∴当
,∴当 ![]() 时,
时,
![]() ,当
,当 ![]() 时,
时, ![]() ,即F(x)在
,即F(x)在 ![]() 单调递减,在
单调递减,在 ![]() 单调递增,故
单调递增,故 ![]() 在
在 ![]() 取最小值
取最小值 ![]() ,
,
而 ![]() .
.
∴当 ![]() 时,
时, ![]() ,即
,即 ![]() 恒成立.
恒成立.
②若 ![]() ,则
,则 ![]() ,
,
∴当 ![]() 时,
时, ![]() ,∴
,∴ ![]() 在
在 ![]() 单调递增,
单调递增,
而 ![]() ,∴当
,∴当 ![]() 时,
时, ![]() ,即
,即 ![]() 恒成立,
恒成立,
③若 ![]() ,则
,则 ![]() ,
,
∴当 ![]() 时,
时, ![]() 不可能恒成立.
不可能恒成立.
综上所述, ![]() 的取值范围为
的取值范围为 ![]()
【解析】(1)根据题意f(0)=2,g(0)=2,根据导数的几何意义可知f![]() (0)=4,g
(0)=4,g![]() (0)=4,从而可求得a,b,c,d的值;(2)构造函数 F(x)=kg(x)-f(x) ,若x≥-2时,恒有f(x)≤kg(x),即证 x ≥ 2 时恒有 F ( x ) ≥ 0 .先将函数 F(x)=kg(x)-f(x)求导,讨论导数的正负得函数的增减区间,根据函数的单调性求其最值.使其最小值大于等于0即可.
(0)=4,从而可求得a,b,c,d的值;(2)构造函数 F(x)=kg(x)-f(x) ,若x≥-2时,恒有f(x)≤kg(x),即证 x ≥ 2 时恒有 F ( x ) ≥ 0 .先将函数 F(x)=kg(x)-f(x)求导,讨论导数的正负得函数的增减区间,根据函数的单调性求其最值.使其最小值大于等于0即可.
【考点精析】利用导数的几何意义和函数的最大(小)值与导数对题目进行判断即可得到答案,需要熟知通过图像,我们可以看出当点![]() 趋近于
趋近于![]() 时,直线
时,直线![]() 与曲线相切.容易知道,割线
与曲线相切.容易知道,割线![]() 的斜率是
的斜率是![]() ,当点
,当点![]() 趋近于
趋近于![]() 时,函数
时,函数![]() 在
在![]() 处的导数就是切线PT的斜率k,即
处的导数就是切线PT的斜率k,即![]() ;求函数
;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设不经过坐标原点
 的直线
的直线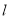 与圆
与圆 交于不同的两点
交于不同的两点 .若直线
.若直线 的斜率与直线
的斜率与直线 和
和 斜率满足
斜率满足 ,求
,求 面积
面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)解关于
 的不等式
的不等式 ;
;(2)若
 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列
 满足:
满足:  ,
,  .
.(
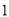 )求
)求 ,
,  ,
,  的值.
的值.(
 )求证:数列
)求证:数列 是等比数列.
是等比数列.(
 )令
)令 ,如果对任意
,如果对任意 ,都有
,都有 ,求实数
,求实数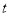 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】36的所有正约数之和可按如下方法得到:因为36=22×32 , 所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可得100的所有正约数之和为( )
A.217
B.273
C.455
D.651 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数集
 具有性质
具有性质 :对任意的
:对任意的
 ,
, ,使得
,使得 成立.
成立.(Ⅰ)分别判断数集
 与
与 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(Ⅱ)求证
 ;
;(Ⅲ)若
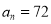 ,求数集
,求数集 中所有元素的和的最小值.
中所有元素的和的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】有下列命题:
①函数
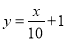 的图象与
的图象与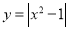 的图象恰有
的图象恰有 个公共点;
个公共点;②函数
 有
有 个零点;
个零点;③若函数
 与
与 的图像关于直线
的图像关于直线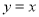 对称,则函数
对称,则函数 与
与 的图象也关于直线
的图象也关于直线 对称;
对称;④函数
 的图象是由函数
的图象是由函数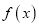 的图象水平向右平移一个单位后,将所得图象在
的图象水平向右平移一个单位后,将所得图象在 轴右侧部分沿
轴右侧部分沿 轴翻折到
轴翻折到 轴左侧替代
轴左侧替代 轴左侧部分图象,并保留右侧部分而得到的.其中错误的命题有___________.(填写所有错误的命题的序号)
轴左侧部分图象,并保留右侧部分而得到的.其中错误的命题有___________.(填写所有错误的命题的序号)
相关试题

