【题目】已知数列![]() 满足:
满足: ![]() ,
, ![]() .
.
(![]() )求
)求![]() ,
, ![]() ,
, ![]() 的值.
的值.
(![]() )求证:数列
)求证:数列![]() 是等比数列.
是等比数列.
(![]() )令
)令![]() ,如果对任意
,如果对任意![]() ,都有
,都有![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() ,
, ![]() ,
, ![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】试题分析:
(1)根据递推关系求值即可.(2)由递推关系可得![]() ,与原式相减可得
,与原式相减可得![]() ,即
,即![]() ,于是可得数列
,于是可得数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列.(3)由(
为公比的等比数列.(3)由(![]() )可得
)可得![]() ,故
,故![]() ,作差判断可得数列
,作差判断可得数列![]() 前三项递增,从第四项开始递减,于是可得数列的最大项为
前三项递增,从第四项开始递减,于是可得数列的最大项为![]() .由题意可得
.由题意可得![]() 恒成立,于是
恒成立,于是![]() ,解不等式可得所求范围.
,解不等式可得所求范围.
试题解析:
(![]() )由题意,
)由题意, ![]() ,
, ![]() ,
, ![]() ,
,
计算可得![]() ,
, ![]() ,
, ![]() .
.
(![]() )由题意可得,
)由题意可得, ![]() ,
,
![]() ,
,
两式相减得![]() ,
,
即![]() ,
,
∴![]() ,
,
又![]() ,
,
∴数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公比的等比数列.
为公比的等比数列.
(![]() )由(
)由(![]() )可得
)可得![]() ,
,
∴![]() ,
,
∴![]() ,
,
由![]() ,得
,得![]() ;
;
由![]() 可得
可得![]() ,
,
∴![]() ,
,
∴数列![]() 有最大值
有最大值![]() ,
,
∴对任意![]() ,有
,有![]() ,
,
∵对任意的![]() ,有
,有![]() ,即
,即![]() 恒成立,
恒成立,
∴![]() ,整理得
,整理得![]()
解得![]() 或
或![]() .
.
∴实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】三棱锥
 中,侧面
中,侧面 与底面
与底面 垂直,
垂直,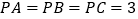 .
.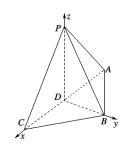
(1)求证:
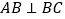 ;
;(2)设
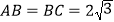 ,求
,求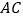 与平面
与平面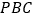 所成角的大小.
所成角的大小. -
科目: 来源: 题型:
查看答案和解析>>【题目】设不经过坐标原点
 的直线
的直线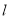 与圆
与圆 交于不同的两点
交于不同的两点 .若直线
.若直线 的斜率与直线
的斜率与直线 和
和 斜率满足
斜率满足 ,求
,求 面积
面积 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)解关于
 的不等式
的不等式 ;
;(2)若
 在区间
在区间 上恒成立,求实数
上恒成立,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+ax+b , g(x)=ex(cx+d),若曲线y=f(x)和曲线y=g(x)都过点P(0,2),且在点P处有相同的切线y=4x+2.
(1)求a , b , c , d的值;
(2)若x≥-2时,恒有f(x)≤kg(x),求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】36的所有正约数之和可按如下方法得到:因为36=22×32 , 所以36的所有正约数之和为(1+3+32)+(2+2×3+2×32)+(22+22×3+22×32)=(1+2+22)(1+3+32)=91,参照上述方法,可得100的所有正约数之和为( )
A.217
B.273
C.455
D.651 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知数集
 具有性质
具有性质 :对任意的
:对任意的
 ,
, ,使得
,使得 成立.
成立.(Ⅰ)分别判断数集
 与
与 是否具有性质
是否具有性质 ,并说明理由;
,并说明理由;(Ⅱ)求证
 ;
;(Ⅲ)若
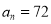 ,求数集
,求数集 中所有元素的和的最小值.
中所有元素的和的最小值.
相关试题

