【题目】已知点 ![]() ,点P是圆
,点P是圆 ![]() 上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
(1)求点E的轨迹方程;
(2)已知M,N两点的坐标分别为(﹣2,0),(2,0),点T是直线x=4上的一个动点,且直线TM,TN分别交(1)中点E的轨迹于C,D两点(M,N,C,D四点互不相同),证明:直线CD恒过一定点,并求出该定点坐标.
参考答案:
【答案】
(1)解:∵|EA|+|QE|=|EQ|+|PE|=4,且|QA|=2 ![]() <4,
<4,
∴点E的轨迹是以A,Q为焦点的椭圆,
设椭圆方程为 ![]() =1,则2a=4,c=
=1,则2a=4,c= ![]() ,∴a=2,b=
,∴a=2,b= ![]() =1.
=1.
所以点E的轨迹方程为: ![]()
(2)解:依题意设直线CD的方程为:x=my+n,
代入椭圆方程x2+4y2=4得:(4+m2)y2+2mny+(n2﹣4)=0
设C(x1,y1),D(x2,y2),则 ![]() ,
, ![]() .
.
∵直线TM方程为 ![]() ,直线TN方程为
,直线TN方程为 ![]() ,
,
由题知TM,TN的交点T的横坐标为4,∴ ![]() ,即3y1(x2﹣2)=y2(x1+2),
,即3y1(x2﹣2)=y2(x1+2),
即:3y1(my2+n﹣2)=y2(my1+n+2),整理得:2my1y2=(n+2)y2﹣3(n﹣2)y1,
∴ ![]()
化简可得: ![]() .
.
∵当m,y1变化时,上式恒成立,∴n=1,
∴直线CD恒过一定点(1,0)
【解析】(1)利用椭圆的定义即可得出E的轨迹方程;(2)设CD方程x=my+n,代入椭圆方程消元,得出C,D坐标的关系,求出TM,TN的方程,根据交点横坐标为4得出恒等式,从而得出n的值,即得出直线CD的定点坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】朱载堉(1536~1611),是中国明代一位杰出的音乐家、数学家和天文历算家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度13个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为
 ,第七个音的频率为
,第七个音的频率为 ,则
,则 =
=A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
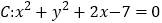 内一点
内一点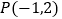 ,直线
,直线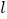 过点
过点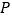 且与圆
且与圆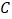 交于
交于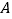 ,
,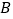 两点.
两点.(1)求圆
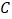 的圆心坐标和面积;
的圆心坐标和面积;(2)若直线
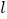 的斜率为
的斜率为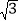 ,求弦
,求弦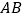 的长;
的长;(3)若圆上恰有三点到直线
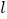 的距离等于
的距离等于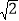 ,求直线
,求直线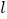 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】一袋中装有10个大小相同的黑球和白球.已知从袋中任意摸出2个球,至少得到1个白球的概率是
 .
.(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为
 ,求随机变量
,求随机变量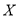 的分布列.
的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣ax+a(a∈R),其中e为自然对数的底数.
(1)讨论函数y=f(x)的单调性;
(2)函数y=f(x)的图象与x轴交于A(x1 , 0),B(x2 , 0)两点,x1<x2 , 点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记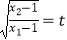 ,求at﹣(a+t)的值.
,求at﹣(a+t)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的参数方程为
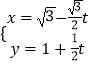 (t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为  .
.
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面 的公共点,求
的公共点,求  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理” 的原则,规定参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有
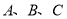 三家社区医院,并且他们的选择是等可能的、相互独立的.
三家社区医院,并且他们的选择是等可能的、相互独立的.(1)求甲、乙两人都选择
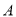 社区医院的概率;
社区医院的概率;(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设在4名参加保险人员中选择
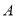 社区医院的人数为
社区医院的人数为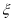 ,求
,求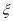 的分布列和数学期望及方差.
的分布列和数学期望及方差.
相关试题

