【题目】一袋中装有10个大小相同的黑球和白球.已知从袋中任意摸出2个球,至少得到1个白球的概率是![]() .
.
(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为![]() ,求随机变量
,求随机变量![]() 的分布列.
的分布列.
参考答案:
【答案】(1)5;(2)答案见解析.
【解析】试题分析:(1)设黑球的个数为x,则白球的个数为10-x,记两个都是黑球得的事件为A,则至少有一个白球的事件与事件A为对立事件,由此能求出白球的个数;
(2)X服从超几何分布,其中N=10,M=5,n=3,其中P(X=k)=![]() ,k=0,1,2,3.
,k=0,1,2,3.
可求得分布列及数学期望.
试题解析:
(1)记“从袋中任意摸出2个球,至少得到1个白球”为事件A,
设袋中白球的个数为x,
则P(A)=1-![]() =
=![]() ,得到x=5.
,得到x=5.
(2)X服从超几何分布,其中N=10,M=5,n=3,其中P(X=k)=![]() ,k=0,1,2,3.
,k=0,1,2,3.
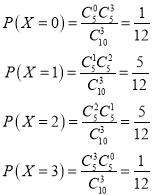
于是可得其分布列为
X | 0 | 1 | 2 | 3 |
P |
|
|
|
|
X的数学期望
E(X)=![]() ×0+
×0+![]() ×1+
×1+![]() ×2+
×2+![]() ×3=
×3=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】棉花的纤维长度是评价棉花质量的重要指标,某农科所的专家在土壤环境不同的甲、乙两块实验地分别种植某品种的棉花,为了评价该品种的棉花质量,在棉花成熟后,分别从甲、乙两地的棉花中各随机抽取20根棉花纤维进行统计,结果如下表:(记纤维长度不低于300mm的为“长纤维”,其余为“短纤维”)
纤维长度
(0,100)
[100,200)
[200,300)
[300,400)
[400,500]
甲地(根数)
3
4
4
5
4
乙地(根数)
1
1
2
10
6
(1)由以上统计数据,填写下面2×2列联表,并判断能否在犯错误概率不超过0.025的前提下认为“纤维长度与土壤环境有关系”.甲地
乙地
总计
长纤维
短纤维
总计
附:(1)
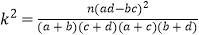 ;(2)临界值表;
;(2)临界值表;P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
(2)现从上述40根纤维中,按纤维长度是否为“长纤维”还是“短纤维”采用分层抽样的方法抽取8根进行检测,在这8根纤维中,记乙地“短纤维”的根数为X,求X的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】朱载堉(1536~1611),是中国明代一位杰出的音乐家、数学家和天文历算家,他的著作《律学新说》中制成了最早的“十二平均律”.十二平均律是目前世界上通用的把一组音(八度)分成十二个半音音程的律制,各相邻两律之间的频率之比完全相等,亦称“十二等程律”.即一个八度13个音,相邻两个音之间的频率之比相等,且最后一个音是最初那个音的频率的2倍.设第三个音的频率为
 ,第七个音的频率为
,第七个音的频率为 ,则
,则 =
=A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
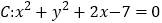 内一点
内一点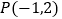 ,直线
,直线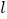 过点
过点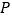 且与圆
且与圆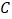 交于
交于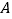 ,
,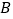 两点.
两点.(1)求圆
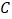 的圆心坐标和面积;
的圆心坐标和面积;(2)若直线
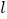 的斜率为
的斜率为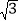 ,求弦
,求弦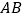 的长;
的长;(3)若圆上恰有三点到直线
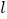 的距离等于
的距离等于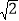 ,求直线
,求直线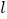 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
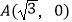 ,点P是圆
,点P是圆 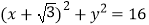 上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
(1)求点E的轨迹方程;
(2)已知M,N两点的坐标分别为(﹣2,0),(2,0),点T是直线x=4上的一个动点,且直线TM,TN分别交(1)中点E的轨迹于C,D两点(M,N,C,D四点互不相同),证明:直线CD恒过一定点,并求出该定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=ex﹣ax+a(a∈R),其中e为自然对数的底数.
(1)讨论函数y=f(x)的单调性;
(2)函数y=f(x)的图象与x轴交于A(x1 , 0),B(x2 , 0)两点,x1<x2 , 点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记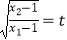 ,求at﹣(a+t)的值.
,求at﹣(a+t)的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的参数方程为
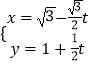 (t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为  .
.
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面 的公共点,求
的公共点,求  的取值范围.
的取值范围.
相关试题

