【题目】已知函数f(x)=ex﹣ax+a(a∈R),其中e为自然对数的底数.
(1)讨论函数y=f(x)的单调性;
(2)函数y=f(x)的图象与x轴交于A(x1 , 0),B(x2 , 0)两点,x1<x2 , 点C在函数y=f(x)的图象上,且△ABC为等腰直角三角形,记 ![]() ,求at﹣(a+t)的值.
,求at﹣(a+t)的值.
参考答案:
【答案】
(1)解:函数f(x)=ex﹣ax+a,f'(x)=ex﹣a,
①当a≤0时,则f'(x)>0,则函数f(x)在(﹣∞,+∞)是单调增函数.
②当a>0时,令f'(x)=0,则x=lna,
若x<lna,f'(x)<0,所以f(x)在(﹣∞,lna)上是单调减函数;
若x>lna,f'(x)>0,所以f(x)在(lna,+∞)上是单调增函数.
(2)解:由(1)可知当a>0时,函数y=f(x)其图象与x轴交于两点,则有 ![]() ,则
,则 ![]() ,则xi>1(i=1,2).
,则xi>1(i=1,2).
于是 ![]() ,在等腰三角形ABC中,显然C=90°,所以
,在等腰三角形ABC中,显然C=90°,所以 ![]() ,即y0=f(x0)<0,
,即y0=f(x0)<0,
由直角三角形斜边的中线性质,可知 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
所以 ![]() ,
,
即 ![]() .
.
因为x1﹣1≠0,则 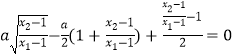 ,
,
又 ![]() ,所以
,所以 ![]() ,
,
即 ![]() ,则(a﹣1)(t﹣1)=2.
,则(a﹣1)(t﹣1)=2.
所以at﹣(a+t)=1.
【解析】(1)求导,分类讨论,根据导数与函数单调性的关系,即可求得f(x)的单调性区间;(2)由题意可知:C=90°,则 ![]() ,即y0=f(x0)<0,然后得到关于参数a的方程
,即y0=f(x0)<0,然后得到关于参数a的方程 ![]() ,则
,则 ![]() ,则(a﹣1)(t﹣1)=2.即可求得at﹣(a+t)=1.
,则(a﹣1)(t﹣1)=2.即可求得at﹣(a+t)=1.
【考点精析】本题主要考查了利用导数研究函数的单调性的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减才能正确解答此题.
在这个区间单调递减才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
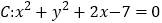 内一点
内一点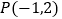 ,直线
,直线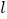 过点
过点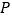 且与圆
且与圆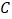 交于
交于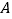 ,
,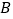 两点.
两点.(1)求圆
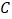 的圆心坐标和面积;
的圆心坐标和面积;(2)若直线
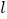 的斜率为
的斜率为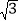 ,求弦
,求弦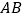 的长;
的长;(3)若圆上恰有三点到直线
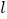 的距离等于
的距离等于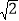 ,求直线
,求直线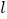 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】一袋中装有10个大小相同的黑球和白球.已知从袋中任意摸出2个球,至少得到1个白球的概率是
 .
.(1)求白球的个数;
(2)从袋中任意摸出3个球,记得到白球的个数为
 ,求随机变量
,求随机变量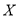 的分布列.
的分布列. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点
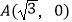 ,点P是圆
,点P是圆 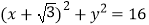 上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
上的任意一点,设Q为该圆的圆心,并且线段PA的垂直平分线与直线PQ交于点E.
(1)求点E的轨迹方程;
(2)已知M,N两点的坐标分别为(﹣2,0),(2,0),点T是直线x=4上的一个动点,且直线TM,TN分别交(1)中点E的轨迹于C,D两点(M,N,C,D四点互不相同),证明:直线CD恒过一定点,并求出该定点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的参数方程为
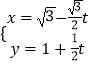 (t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为
(t为参数),以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,圆C的极坐标方程为  .
.
(1)求圆C的直角坐标方程;
(2)若P(x,y)是直线l与圆面 的公共点,求
的公共点,求  的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某市医疗保险实行定点医疗制度,按照“就近就医、方便管理” 的原则,规定参加保险人员可自主选择四家医疗保险定点医院和一家社区医院作为就诊的医疗机构.若甲、乙、丙、丁4名参加保险人员所在地区附近有
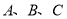 三家社区医院,并且他们的选择是等可能的、相互独立的.
三家社区医院,并且他们的选择是等可能的、相互独立的.(1)求甲、乙两人都选择
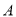 社区医院的概率;
社区医院的概率;(2)求甲、乙两人不选择同一家社区医院的概率;
(3)设在4名参加保险人员中选择
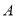 社区医院的人数为
社区医院的人数为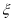 ,求
,求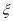 的分布列和数学期望及方差.
的分布列和数学期望及方差. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值.
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;
(2)直线l1与直线l2平行,并且坐标原点到l1,l2的距离相等.
相关试题

