【题目】解答
(1)若关于x的不等式﹣ ![]() +2x>mx的解集为(0,2),求m的值.
+2x>mx的解集为(0,2),求m的值.
(2)在△ABC中,sinA= ![]() ,cosB=
,cosB= ![]() ,求cosC的值.
,求cosC的值.
参考答案:
【答案】
(1)解:若关于x的不等式﹣ ![]() +2x>mx的解集为(0,2),
+2x>mx的解集为(0,2),
则0,2是﹣ ![]() +2x=mx的解,
+2x=mx的解,
故﹣ ![]() ×22+2×2=2m,解得:m=1,
×22+2×2=2m,解得:m=1,
所以:m=1,
(2)解:在△ABC中,由cosB= ![]() 可得,sinB=
可得,sinB= ![]() .而sinA=
.而sinA= ![]() <sinB,
<sinB,
由正弦定理可得a<b,∴A<B,
所以A为锐角,cosA= ![]() =
= ![]() ,
,
于是cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB=﹣ ![]()
【解析】(1)将2代入方程﹣ ![]() +2x=mx,求出m的值即可;(2)利用同角三角函数的基本关系求出sinB 的值,而由sinA=
+2x=mx,求出m的值即可;(2)利用同角三角函数的基本关系求出sinB 的值,而由sinA= ![]() <sinB,可得 A<B,故A为锐角,从而求得cosA 的值,再由cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB 求出结果.
<sinB,可得 A<B,故A为锐角,从而求得cosA 的值,再由cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB 求出结果.
【考点精析】根据题目的已知条件,利用解一元二次不等式和两角和与差的余弦公式的相关知识可以得到问题的答案,需要掌握求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;两角和与差的余弦公式:
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边;两角和与差的余弦公式:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
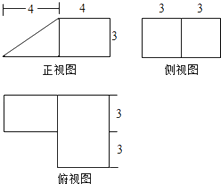
A.90cm2
B.129cm2
C.132cm2
D.138cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=alnx+1(a>0).
(1)当x>0时,求证: ;
;
(2)在区间(1,e)上f(x)>x恒成立,求实数a的范围.
(3)当 时,求证:
时,求证:  (n∈N*).
(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数
 (份)与收入
(份)与收入 (元)之间有如下的对应数据:
(元)之间有如下的对应数据:外卖份数
 (份)
(份)2
4
5
6
8
收入
 (元)
(元)30
40
60
50
70

(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式
 ,
,  ;
;②参考数据:
 ,
,  ,
,  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1 , F2分别为双曲线
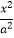 ﹣
﹣ 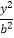 =1(a>0,b>0)的左右焦点,如果双曲线上存在一点P,使得F2关于直线PF1的对称点恰在y轴上,则该双曲线的离心率e的取值范围为( )
=1(a>0,b>0)的左右焦点,如果双曲线上存在一点P,使得F2关于直线PF1的对称点恰在y轴上,则该双曲线的离心率e的取值范围为( )
A.e>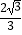
B.1<e<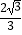
C.e>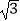
D.1<e<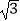
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( )
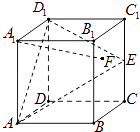
A.{t|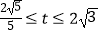 }
}
B.{t|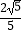 ≤t≤2}??
≤t≤2}??
C.{t|2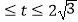 }
}
D.{t|2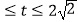 }
} -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}满足:a3=4,a5+a7=14,{an}的前n项和为Sn .
(1)求an及Sn;
(2)令bn= (n∈N*),求数列{bn}的前n项和Tn .
(n∈N*),求数列{bn}的前n项和Tn .
相关试题

