【题目】某特色餐馆开通了美团外卖服务,在一周内的某特色菜外卖份数![]() (份)与收入
(份)与收入![]() (元)之间有如下的对应数据:
(元)之间有如下的对应数据:
外卖份数 | 2 | 4 | 5 | 6 | 8 |
收入 | 30 | 40 | 60 | 50 | 70 |

(1)画出散点图;
(2)求回归直线方程;
(3)据此估计外卖份数为12份时,收入为多少元.
注:①参考公式:线性回归方程系数公式 ,
, ![]() ;
;
②参考数据: ![]() ,
, ![]() ,
, ![]() .
.
参考答案:
【答案】(1)见解析(2)![]() ;(3)95.5元.
;(3)95.5元.
【解析】试题分析:(1)根据表中数据,作出散点图即可;
(2)计算![]() 、
、![]() ,求出回归系数,写出回归直线方程;
,求出回归系数,写出回归直线方程;
(3)由回归直线方程,计算x=12时![]() 的值即可.
的值即可.
试题解析: (1)作出散点图如下图所示:

(2)![]() ,
,
![]() ,
,
已知![]() ,
, ![]() .
.
由公式 ,
, ![]() ,可求得
,可求得![]() ,
, ![]() ,
,
因此回归直线方程为![]() ;
;
(3)![]() 时,
时, ![]() .
.
即外卖份数为12份时,收入大约为95.5元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M为△ABC的中线AD的中点,过点M的直线分别交两边AB、AC于点P、Q,设
 =x
=x  ,
,  ,记y=f(x).
,记y=f(x).
(1)求函数y=f(x)的表达式;
(2)设g(x)=x3+3a2x+2a,x∈[0,1].若对任意x1∈[ ,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围.
,1],总存在x2∈[0,1],使得f(x1)=g(x2)成立,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】某几何体的三视图(单位:cm)如图所示,则此几何体的表面积是( )
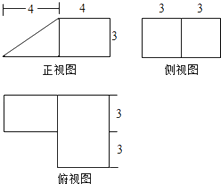
A.90cm2
B.129cm2
C.132cm2
D.138cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=alnx+1(a>0).
(1)当x>0时,求证: ;
;
(2)在区间(1,e)上f(x)>x恒成立,求实数a的范围.
(3)当 时,求证:
时,求证:  (n∈N*).
(n∈N*). -
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)若关于x的不等式﹣ +2x>mx的解集为(0,2),求m的值.
+2x>mx的解集为(0,2),求m的值.
(2)在△ABC中,sinA= ,cosB=
,cosB= 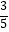 ,求cosC的值.
,求cosC的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知F1 , F2分别为双曲线
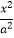 ﹣
﹣ 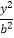 =1(a>0,b>0)的左右焦点,如果双曲线上存在一点P,使得F2关于直线PF1的对称点恰在y轴上,则该双曲线的离心率e的取值范围为( )
=1(a>0,b>0)的左右焦点,如果双曲线上存在一点P,使得F2关于直线PF1的对称点恰在y轴上,则该双曲线的离心率e的取值范围为( )
A.e>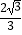
B.1<e<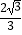
C.e>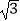
D.1<e<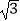
-
科目: 来源: 题型:
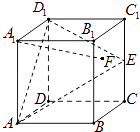
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,E是棱CC1的中点,F是侧面BCC1B1内的动点,且A1F∥平面D1AE,则A1F与平面BCC1B1所成角的正切值t构成的集合是( )
A.{t|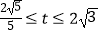 }
}
B.{t|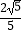 ≤t≤2}??
≤t≤2}??
C.{t|2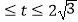 }
}
D.{t|2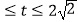 }
}
相关试题

