【题目】已知椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
直线![]() 与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一点,若过点![]() 的直线
的直线![]() 与椭圆C相交于不同的两点S和T,
与椭圆C相交于不同的两点S和T,
满足![]() (O为坐标原点),求实数
(O为坐标原点),求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】试题分析:(1)设椭圆的方程,用待定系数法求出![]() 的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式
的值;(2)解决直线和椭圆的综合问题时注意:第一步:根据题意设直线方程,有的题设条件已知点,而斜率未知;有的题设条件已知斜率,点不定,可由点斜式设直线方程.第二步:联立方程:把所设直线方程与椭圆的方程联立,消去一个元,得到一个一元二次方程.第三步:求解判别式![]() :计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论..
:计算一元二次方程根.第四步:写出根与系数的关系.第五步:根据题设条件求解问题中结论..
试题解析:(Ⅰ)由题意,以椭圆![]() 的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为
的右焦点为圆心,以椭圆的长半轴长为半径的圆的方程为![]() ,
,
∴圆心到直线![]() 的距离
的距离![]() (*)
(*)
∵椭圆![]() 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,
∴![]() ,
,![]() , 代入(*)式得
, 代入(*)式得![]() ,∴
,∴![]() ,
,
故所求椭圆方程为![]()
(Ⅱ)由题意知直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程为
方程为![]() ,设
,设![]() ,
,
将直线方程代入椭圆方程得:![]() ,
,
∴![]() ,∴
,∴![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,
由![]() ,
,
当![]() ,直线
,直线![]() 为
为![]() 轴,
轴, ![]() 点在椭圆上适合题意;
点在椭圆上适合题意;
当![]() ,得
,得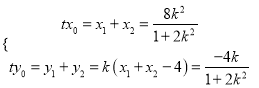 ∴
∴![]()
![]()
![]() .
.
将上式代入椭圆方程得:![]() ,
,
整理得:![]() ,由
,由![]() 知,
知,![]() ,所以
,所以![]() ,
,
综上可得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需要看不同类型的书籍,为了合理配备资源,现对小区看书人员进行年龄调查,随机抽取了一天40名读书者进行调查,将他们的年龄分成6段:
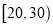 ,
, 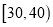 ,
, 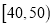 ,
, 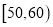 ,
, 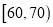 ,
, 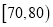 后得到如图所示的频率分布直方图,问:
后得到如图所示的频率分布直方图,问: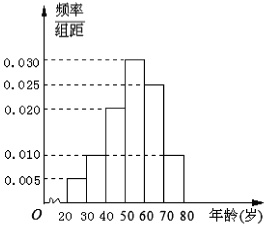
(1)在40名读书者中年龄分布在
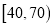 的人数;
的人数;(2)估计40名读书者年龄的平均数和中位数;
(3)若从年龄在
 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在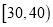 的人数
的人数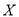 的分布列和数学期望.
的分布列和数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当
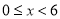 时,y是x的二次函数;当
时,y是x的二次函数;当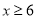 时,
时,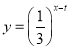 测得数据如下表(部分):
测得数据如下表(部分):x(单位:克)
0
1
2
9
…
y
0
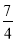
3
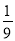
…
(1)求y关于x的函数关系式
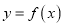 ;
;(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
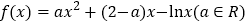 ,又
,又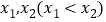 恰为
恰为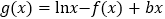 的零点.
的零点.(1)当
 时,求
时,求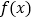 的单调区间;
的单调区间;(2)当
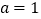 时,求证
时,求证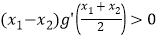
-
科目: 来源: 题型:
查看答案和解析>>【题目】【2018安徽淮南市高三一模(2月)】已知函数
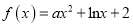 .
.(I)若
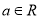 ,讨论函数
,讨论函数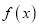 的单调性;
的单调性;(II)曲线
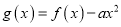 与直线
与直线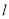 交于
交于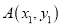 ,
, 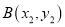 两点,其中
两点,其中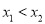 ,若直线
,若直线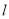 斜率为
斜率为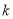 ,求证:
,求证: 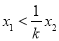 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的函数f(x)满足:对任意
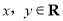 都有
都有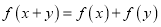 ,且当x>0时,
,且当x>0时,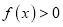 .
.(1)求
 的值,并证明
的值,并证明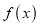 为奇函数;
为奇函数;(2)判断函数
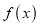 的单调性,并证明;
的单调性,并证明;(3)若
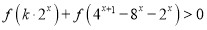 对任意
对任意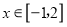 恒成立,求实数
恒成立,求实数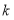 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知射手甲射击一次,命中9环(含9环)以上的概率为0.56,命中8环的概率为0.22,命中7环的概率为0.12.
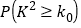
0.50
0.40
0.25
0.15
0.10
0.05
0.025
0.010
0.005
0.001
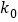
0.455
0.708
1.323
2.072
2.706
3.841
5.024
6.635
7.879
10.828
(1)求甲射击一次,命中不足8环的概率;
(2)求甲射击一次,至少命中7环的概率.
相关试题

