【题目】某小区为了提高小区内人员的读书兴趣,特举办读书活动,准备进一定量的书籍丰富小区图书站,由于不同年龄段需要看不同类型的书籍,为了合理配备资源,现对小区看书人员进行年龄调查,随机抽取了一天40名读书者进行调查,将他们的年龄分成6段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图所示的频率分布直方图,问:
后得到如图所示的频率分布直方图,问:
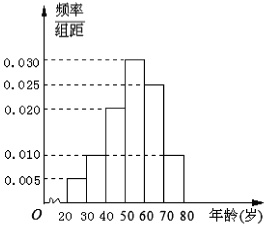
(1)在40名读书者中年龄分布在![]() 的人数;
的人数;
(2)估计40名读书者年龄的平均数和中位数;
(3)若从年龄在![]() 的读书者中任取2名,求这两名读书者年龄在
的读书者中任取2名,求这两名读书者年龄在![]() 的人数
的人数![]() 的分布列和数学期望.
的分布列和数学期望.
参考答案:
【答案】(1)30;(2)平均数为54,中位数为55;(3)答案见解析.
【解析】试题分析:(1)由频率分布直方图知年龄在[40,70)的频率为0.75,由此能求出40名读书者中年龄分布在![]() 的人数.
的人数.
(2)利用频率分布直方图能求出40名读书者年龄的平均数和中位数.
(3)年龄在![]() 的读书者有2人,年龄在
的读书者有2人,年龄在![]() 的读书者有4人,设年龄在
的读书者有4人,设年龄在![]() 的读书者人数为X,由此能求出恰有1名读书者年龄在[30,40)的概率.
的读书者人数为X,由此能求出恰有1名读书者年龄在[30,40)的概率.
试题解析:
(1)由频率分布直方图知年龄在![]() 的频率为
的频率为![]() ,所以40名读书者中年龄分布在
,所以40名读书者中年龄分布在![]() 的人数为
的人数为![]() .
.
(2)40名读书者年龄的平均数为
![]() ,
,
设中位数为![]() ,则
,则![]() ,解得
,解得![]() .
.
即40名读书者年龄的中位数为55.
(3)年龄在![]() 的读书者有
的读书者有![]() 人,年龄在
人,年龄在![]() 的读书者有
的读书者有![]() 人,所以
人,所以![]() 的所有可能取值有0,1,2.
的所有可能取值有0,1,2.
![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分布列如下:
的分布列如下:
| 0 | 1 | 2 |
|
|
|
|
数学期望![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )

A. 5 B. 6 C. 7 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】设命题
 “关于
“关于 的不等式
的不等式 对任意
对任意 恒成立”,命题
恒成立”,命题 “函数
“函数 在区间
在区间 上是增函数”.
上是增函数”.(1)若
 为真,求实数
为真,求实数 的取值范围;
的取值范围;(2)若
 为假,
为假, 为真,求实数
为真,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 经过点
经过点 ,且两焦点与短轴的一个端点构成等腰直角三角形.
,且两焦点与短轴的一个端点构成等腰直角三角形. (Ⅰ)求椭圆的方程;
(Ⅱ)若圆
 的任意一条切线
的任意一条切线 与椭圆E相交于P,Q两点,试问:
与椭圆E相交于P,Q两点,试问: 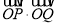 是否为定值? 若是,求这个定值;若不是,说明理由.
是否为定值? 若是,求这个定值;若不是,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年1月8日,中共中央国务院隆重举行国家科学技术奖励大会,在科技界引发热烈反响,自主创新正成为引领经济社会发展的强劲动力.某科研单位在研发新产品的过程中发现了一种新材料,由大数据测得该产品的性能指标值y与这种新材料的含量x(单位:克)的关系为:当
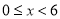 时,y是x的二次函数;当
时,y是x的二次函数;当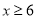 时,
时,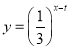 测得数据如下表(部分):
测得数据如下表(部分):x(单位:克)
0
1
2
9
…
y
0
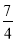
3
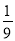
…
(1)求y关于x的函数关系式
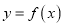 ;
;(2)当该产品中的新材料含量x为何值时,产品的性能指标值最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
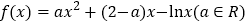 ,又
,又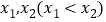 恰为
恰为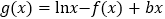 的零点.
的零点.(1)当
 时,求
时,求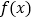 的单调区间;
的单调区间;(2)当
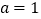 时,求证
时,求证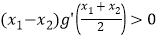
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的两焦点与短轴的一个端点的连线构成等腰直角三角形,
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
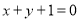 与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.
与以椭圆C的右焦点为圆心,以椭圆的长半轴长为半径的圆相切.(Ⅰ)求椭圆C的方程;
(Ⅱ)设P为椭圆C上一点,若过点
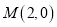 的直线
的直线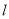 与椭圆C相交于不同的两点S和T,
与椭圆C相交于不同的两点S和T,满足
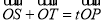 (O为坐标原点),求实数
(O为坐标原点),求实数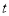 的取值范围.
的取值范围.
相关试题

