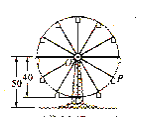
【题目】如图所示,摩天轮的半径为![]() 米,点
米,点![]() 距地面高度为
距地面高度为![]() 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每![]() 分钟转一圈,以点
分钟转一圈,以点![]() 为原点,过点
为原点,过点![]() 且平行与地平线的直线为
且平行与地平线的直线为![]() 轴建立平面直角坐标系
轴建立平面直角坐标系![]() ,设点
,设点![]() 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻![]() (分钟)时点
(分钟)时点![]() 距地面的高度
距地面的高度![]() (米),则
(米),则![]() 与
与![]() 的函数关系式
的函数关系式
![]()
![]() __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点![]() 到地面的距离不小于
到地面的距离不小于![]() 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)
参考答案:
【答案】 ![]() 1
1
【解析】由图形知,可以以点O为原点,OP所在直线为y轴,与OP垂直的向右的方向为x轴建立坐标系,由题意![]() ,A=40,T=3,可得
,A=40,T=3,可得![]() ,故有点P离地面的高度,即t时刻点P离地面的高度
,故有点P离地面的高度,即t时刻点P离地面的高度![]() (2)令
(2)令![]() >70,即解得1<t<2,在旋转一圈的三分钟的时间里,从一分钟开始高度大于70,二分钟开始高度小于70,故高度大于70的时间一周中有一分钟.
>70,即解得1<t<2,在旋转一圈的三分钟的时间里,从一分钟开始高度大于70,二分钟开始高度小于70,故高度大于70的时间一周中有一分钟.
故答案为:
(1)![]() ;
;
(2)一分钟.
-
科目: 来源: 题型:
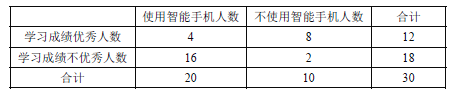
查看答案和解析>>【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
参考数据:

参考公式:
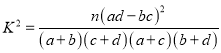 ,其中
,其中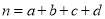
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为
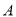 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为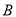 组,计划从
组,计划从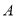 组推选的2人和
组推选的2人和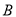 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自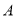 、
、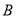 两组的概率.
两组的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
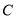 的两个焦点坐标分别是
的两个焦点坐标分别是 ,并且经过
,并且经过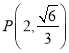 .
.(1)求椭圆
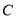 的标准方程;
的标准方程;(2)过椭圆
 的右焦点
的右焦点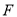 作直线
作直线 ,直线
,直线 与椭圆
与椭圆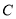 相交于
相交于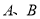 两点,当
两点,当 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(Ⅰ)求
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(Ⅱ)说明函数
 的图像可由正弦曲线
的图像可由正弦曲线 经过怎样的变化得到;
经过怎样的变化得到;(Ⅲ)若
 是第二象限的角,求
是第二象限的角,求
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了
 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(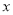 (吨)为该商品进货量,
(吨)为该商品进货量, 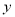 (天)为销售天数):
(天)为销售天数):
(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出
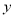 关于
关于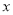 的线性回归方程
的线性回归方程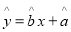 ;
;(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品
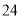 吨,预测需要销售天数;
吨,预测需要销售天数;参考公式和数据:
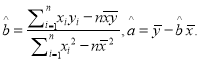
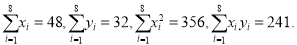
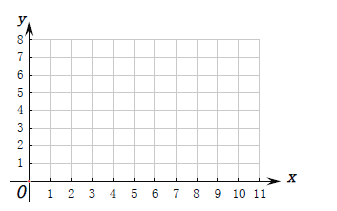
-
科目: 来源: 题型:
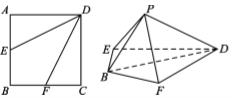
查看答案和解析>>【题目】如图,在边长为2的正方形
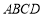 中,点
中,点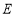 ,
,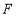 分别是
分别是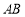 ,
,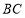 的中点,将
的中点,将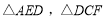 分别沿
分别沿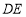 ,
,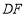 折起,使
折起,使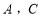 两点重合于
两点重合于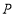 .
.
(Ⅰ)求证:平面
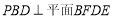 ;
;(Ⅱ)求四棱锥
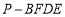 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】过点
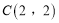 作一直线与抛物线
作一直线与抛物线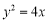 交于
交于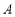 ,
,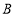 两点,点
两点,点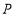 是抛物线
是抛物线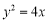 上到直线
上到直线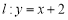 的距离最小的点,直线
的距离最小的点,直线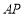 与直线
与直线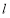 交于点
交于点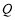 .
.
(Ⅰ)求点
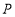 的坐标;
的坐标;(Ⅱ)求证:直线
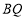 平行于抛物线的对称轴.
平行于抛物线的对称轴.
相关试题

