【题目】某研究型学习小组调查研究”中学生使用智能手机对学习的影响”.部分统计数据如下表:
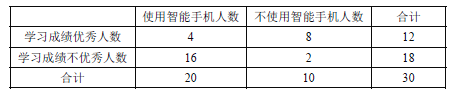
参考数据:

参考公式: 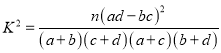 ,其中
,其中![]()
(Ⅰ)试根据以上数据,运用独立性检验思想,指出有多大把握认为中学生使用智能手机对学习有影响?
(Ⅱ)研究小组将该样本中使用智能手机且成绩优秀的4位同学记为![]() 组,不使用智能手机且成绩优秀的8位同学记为
组,不使用智能手机且成绩优秀的8位同学记为![]() 组,计划从
组,计划从![]() 组推选的2人和
组推选的2人和![]() 组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自
组推选的3人中,随机挑选两人在学校升旗仪式上作“国旗下讲话”分享学习经验.求挑选的两人恰好分别来自![]() 、
、![]() 两组的概率.
两组的概率.
参考答案:
【答案】(1)该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响;(2) ![]() .
.
【解析】试题分析:(Ⅰ)根据![]() 列联表,计算
列联表,计算![]() ,对比参考数据,
,对比参考数据, ![]() 且
且![]() ,所以有99.5%的把握认为中学生使用智能手机对学习有影响;(Ⅱ)将
,所以有99.5%的把握认为中学生使用智能手机对学习有影响;(Ⅱ)将![]() 组中的2人,和
组中的2人,和![]() 组中的3人编号,列举所有挑选两人的基本事件的个数,和其中分别来自
组中的3人编号,列举所有挑选两人的基本事件的个数,和其中分别来自![]() 两组的基本事件的个数,最后相除就是所求概率.
两组的基本事件的个数,最后相除就是所求概率.
试题解析:(Ⅰ)根据上方公式求得![]() ,
,
因为![]()
所以该研究小组有99.5%的把握认为中学生使用智能手机对学习有影响.
(Ⅱ)记![]() 组推选的两名同学为
组推选的两名同学为![]() ,
, ![]() 组推选的三名同学为
组推选的三名同学为![]() ,
,
则从中随机选出两名同学包含如下10个基本事件:
![]()
记挑选的两人恰好分别来自![]() 两组为事件
两组为事件![]() ,
,
则事件![]() 包含如下6 个基本事件:
包含如下6 个基本事件:
![]()
故![]() .
.
即挑选的两人恰好分别来自![]() 两组的概率是
两组的概率是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场进行有奖促销活动,顾客购物每满500元,可选择返回50元现金或参加一次抽奖,抽奖规则如下:从1个装有6个白球、4个红球的箱子中任摸一球,摸到红球就可获得100元现金奖励,假设顾客抽奖的结果相互独立.
(Ⅰ)若顾客选择参加一次抽奖,求他获得100元现金奖励的概率;
(Ⅱ)某顾客已购物1500元,作为商场经理,是希望顾客直接选择返回150元现金,还是选择参加3次抽奖?说明理由;
(Ⅲ)若顾客参加10次抽奖,则最有可能获得多少现金奖励?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
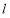 的方程为
的方程为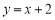 ,点
,点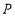 是抛物线
是抛物线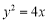 上到直线
上到直线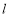 距离最小的点,点
距离最小的点,点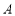 是抛物线上异于点
是抛物线上异于点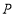 的点,直线
的点,直线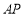 与直线
与直线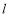 交于点
交于点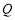 ,过点
,过点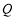 与
与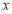 轴平行的直线与抛物线
轴平行的直线与抛物线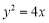 交于点
交于点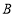 .
.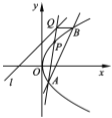
(Ⅰ)求点
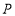 的坐标;
的坐标;(Ⅱ)证明直线
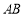 恒过定点,并求这个定点的坐标.
恒过定点,并求这个定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知向量
 ,
,  ,函数
,函数 的图象过点
的图象过点 ,点
,点 与其相邻的最高点的距离为
与其相邻的最高点的距离为 .
.(1)求
 的单调递增区间;
的单调递增区间;(2)计算
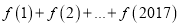 ;
;(3)设函数
 ,试讨论函数
,试讨论函数 在区间
在区间 上的零点个数.
上的零点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
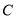 的两个焦点坐标分别是
的两个焦点坐标分别是 ,并且经过
,并且经过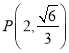 .
.(1)求椭圆
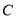 的标准方程;
的标准方程;(2)过椭圆
 的右焦点
的右焦点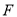 作直线
作直线 ,直线
,直线 与椭圆
与椭圆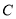 相交于
相交于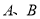 两点,当
两点,当 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(Ⅰ)求
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(Ⅱ)说明函数
 的图像可由正弦曲线
的图像可由正弦曲线 经过怎样的变化得到;
经过怎样的变化得到;(Ⅲ)若
 是第二象限的角,求
是第二象限的角,求
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,摩天轮的半径为
 米,点
米,点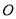 距地面高度为
距地面高度为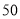 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每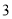 分钟转一圈,以点
分钟转一圈,以点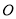 为原点,过点
为原点,过点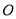 且平行与地平线的直线为
且平行与地平线的直线为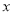 轴建立平面直角坐标系
轴建立平面直角坐标系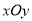 ,设点
,设点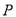 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻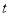 (分钟)时点
(分钟)时点 距地面的高度
距地面的高度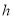 (米),则
(米),则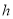 与
与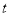 的函数关系式
的函数关系式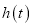
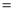 __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点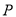 到地面的距离不小于
到地面的距离不小于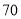 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)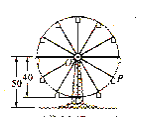
相关试题

