【题目】过点![]() 作一直线与抛物线
作一直线与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 是抛物线
是抛物线![]() 上到直线
上到直线![]() 的距离最小的点,直线
的距离最小的点,直线![]() 与直线
与直线![]() 交于点
交于点![]() .
.

(Ⅰ)求点![]() 的坐标;
的坐标;
(Ⅱ)求证:直线![]() 平行于抛物线的对称轴.
平行于抛物线的对称轴.
参考答案:
【答案】(Ⅰ)![]() (Ⅱ)详见解析
(Ⅱ)详见解析
【解析】
试题分析:(Ⅰ)到直线![]() 距离最小的点,可根据点到直线距离公式,取最小值时的点;也可根据几何意义得为与直线
距离最小的点,可根据点到直线距离公式,取最小值时的点;也可根据几何意义得为与直线![]() 平行且与抛物线相切的切点:如根据点
平行且与抛物线相切的切点:如根据点![]() 到直线
到直线![]() 的距离
的距离
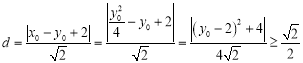 得当且仅当
得当且仅当![]() 时取最小值,(Ⅱ)要证直线
时取最小值,(Ⅱ)要证直线![]() 平行于抛物线的对称轴,就是要证
平行于抛物线的对称轴,就是要证![]() 两点纵坐标相等,设点
两点纵坐标相等,设点![]()
![]() ,求出直线AP方程
,求出直线AP方程![]() ,与直线
,与直线![]() 方程联立,解出点
方程联立,解出点![]() 纵坐标为
纵坐标为![]() .同理求出直线AB方程
.同理求出直线AB方程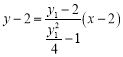 ,与抛物线方程联立,解出点
,与抛物线方程联立,解出点![]() 纵坐标为
纵坐标为![]() .
.
试题解析:(Ⅰ)设点![]() 的坐标为
的坐标为![]() ,则
,则![]() ,
,
所以,点![]() 到直线
到直线![]() 的距离
的距离
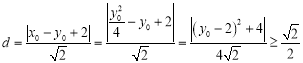 .
.
当且仅当![]() 时等号成立,此时
时等号成立,此时![]() 点坐标为
点坐标为![]() .………………………………4分
.………………………………4分
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,显然
,显然![]() .
.
当![]() 时,
时,![]() 点坐标为
点坐标为![]() ,直线
,直线![]() 的方程为
的方程为![]() ;
;
当![]() 时,直线
时,直线![]() 的方程为
的方程为 ,
,
化简得![]() ;
;
综上,直线![]() 的方程为
的方程为![]() .
.
与直线![]() 的方程
的方程![]() 联立,可得点
联立,可得点![]() 的纵坐标为
的纵坐标为![]() .
.
当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,可得
,可得![]() 点的纵坐标为
点的纵坐标为![]() .
.
此时![]() ,
,
即知![]() 轴,
轴,
当![]() 时,直线
时,直线![]() 的方程为
的方程为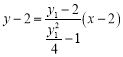 ,
,
化简得![]() ,
,
与抛物线方程![]() 联立,消去
联立,消去![]() ,
,
可得![]() ,
,
所以点![]() 的纵坐标为
的纵坐标为![]() .
.
从而可得![]() 轴,
轴,
所以,![]() 轴.……………………………………13分
轴.……………………………………13分
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,摩天轮的半径为
 米,点
米,点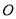 距地面高度为
距地面高度为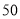 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每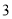 分钟转一圈,以点
分钟转一圈,以点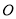 为原点,过点
为原点,过点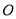 且平行与地平线的直线为
且平行与地平线的直线为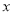 轴建立平面直角坐标系
轴建立平面直角坐标系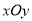 ,设点
,设点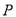 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻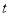 (分钟)时点
(分钟)时点 距地面的高度
距地面的高度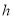 (米),则
(米),则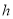 与
与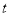 的函数关系式
的函数关系式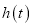
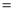 __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点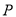 到地面的距离不小于
到地面的距离不小于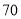 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)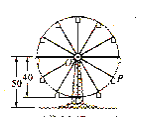
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了
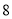 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(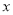 (吨)为该商品进货量,
(吨)为该商品进货量, 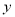 (天)为销售天数):
(天)为销售天数):
(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出
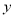 关于
关于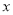 的线性回归方程
的线性回归方程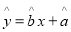 ;
;(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品
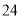 吨,预测需要销售天数;
吨,预测需要销售天数;参考公式和数据:
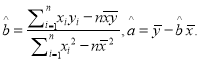
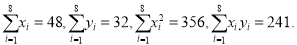
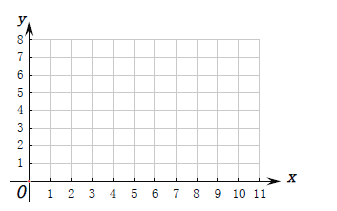
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形
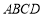 中,点
中,点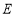 ,
,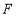 分别是
分别是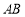 ,
,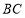 的中点,将
的中点,将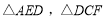 分别沿
分别沿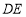 ,
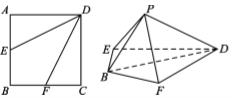
,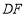 折起,使
折起,使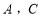 两点重合于
两点重合于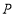 .
.
(Ⅰ)求证:平面
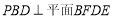 ;
;(Ⅱ)求四棱锥
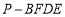 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校对高二年段的男生进行体检,现将高二男生的体重
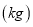 数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组
数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组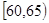 的人数为200.根据一般标准,高二男生体重超过
的人数为200.根据一般标准,高二男生体重超过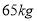 属于偏胖,低于
属于偏胖,低于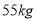 属于偏瘦.观察图形的信息,回答下列问题:
属于偏瘦.观察图形的信息,回答下列问题: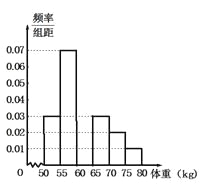
(1)求体重在
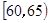 内的频率,并补全频率分布直方图;
内的频率,并补全频率分布直方图;(2)用分层抽样的方法从偏胖的学生中抽取
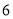 人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?(3)根据频率分布直方图,估计高二男生的体重的中位数与平均数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】集成电路E由3个不同的电子元件组成,现由于元件老化,3个电子元件能正常工作的概率分别降为
 ,
, ,
, ,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。
,且每个电子元件能否正常工作相互独立。若3个电子元件中至少有2个正常工作,则E能正常工作,否则就需要维修,且维修集成电路E所需要费用为100元。(Ⅰ)求集成电路E需要维修的概率;
(Ⅱ)若某电子设备共由2个集成电路E组成,设X为该电子设备需要维修集成电路所需费用。求X的分布列和均值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 ,
,  ,设
,设 .
.(1)求函数
 的最小正周期;
的最小正周期;(2)由
 的图象经过怎样变换得到
的图象经过怎样变换得到 的图象?试写出变换过程;
的图象?试写出变换过程;(3)当
 时,求函数
时,求函数 的最大值及最小值.
的最大值及最小值.
相关试题

