【题目】某商店为了更好地规划某种商品进货的量,该商店从某一年的销售数据中,随机抽取了![]() 组数据作为研究对象,如下图所示(
组数据作为研究对象,如下图所示(![]() (吨)为该商品进货量,
(吨)为该商品进货量, ![]() (天)为销售天数):
(天)为销售天数):

(Ⅰ)根据上表数据在下列网格中绘制散点图:
(Ⅱ)根据上表提供的数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅲ)根据(Ⅱ)中的计算结果,若该商店准备一次性进货该商品![]() 吨,预测需要销售天数;
吨,预测需要销售天数;
参考公式和数据: 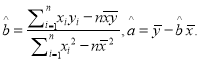
![]()
参考答案:
【答案】(Ⅰ)如解析所示;(Ⅱ) ![]() ;(Ⅲ)17
;(Ⅲ)17
【解析】试题分析:(Ⅰ)根据所给数据画出散点图即可;(Ⅱ)求出中心点的坐标,求出化归方程中的系数,代入方程即可;(Ⅲ)将x的值代入方程求出对应的y的值即可.
试题解析:(Ⅰ)散点图如图所示:
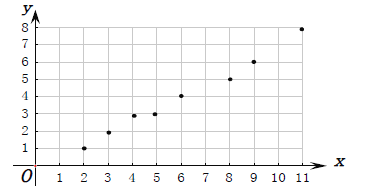
(Ⅱ)依题意, ![]()
![]()
![]()
![]()
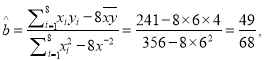
![]()
![]() 回归直线方程为
回归直线方程为![]()
(Ⅲ)由(Ⅱ)知,当![]() 时,
时, ![]()
即若一次性买进蔬菜![]() 吨,则预计需要销售约
吨,则预计需要销售约![]() 天.
天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
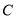 的两个焦点坐标分别是
的两个焦点坐标分别是 ,并且经过
,并且经过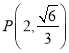 .
.(1)求椭圆
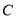 的标准方程;
的标准方程;(2)过椭圆
 的右焦点
的右焦点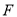 作直线
作直线 ,直线
,直线 与椭圆
与椭圆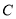 相交于
相交于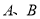 两点,当
两点,当 的面积最大时,求直线
的面积最大时,求直线 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数

(Ⅰ)求
 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;(Ⅱ)说明函数
 的图像可由正弦曲线
的图像可由正弦曲线 经过怎样的变化得到;
经过怎样的变化得到;(Ⅲ)若
 是第二象限的角,求
是第二象限的角,求
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,摩天轮的半径为
 米,点
米,点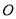 距地面高度为
距地面高度为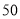 米,摩天轮做匀速运动,每
米,摩天轮做匀速运动,每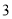 分钟转一圈,以点
分钟转一圈,以点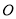 为原点,过点
为原点,过点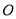 且平行与地平线的直线为
且平行与地平线的直线为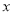 轴建立平面直角坐标系
轴建立平面直角坐标系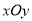 ,设点
,设点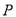 的起始位置在最低点(且在最低点开始时),设在时刻
的起始位置在最低点(且在最低点开始时),设在时刻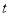 (分钟)时点
(分钟)时点 距地面的高度
距地面的高度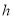 (米),则
(米),则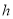 与
与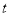 的函数关系式
的函数关系式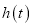
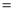 __________.在摩天轮旋转一周内,点
__________.在摩天轮旋转一周内,点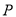 到地面的距离不小于
到地面的距离不小于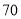 米的时间长度为 __________(分钟)
米的时间长度为 __________(分钟)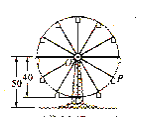
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为2的正方形
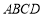 中,点
中,点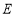 ,
,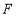 分别是
分别是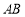 ,
,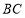 的中点,将
的中点,将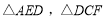 分别沿
分别沿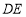 ,
,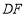 折起,使
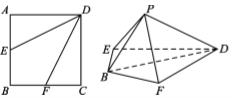
折起,使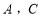 两点重合于
两点重合于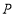 .
.
(Ⅰ)求证:平面
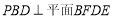 ;
;(Ⅱ)求四棱锥
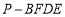 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】过点
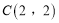 作一直线与抛物线
作一直线与抛物线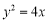 交于
交于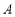 ,
,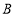 两点,点
两点,点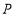 是抛物线
是抛物线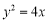 上到直线
上到直线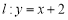 的距离最小的点,直线
的距离最小的点,直线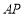 与直线
与直线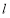 交于点
交于点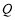 .
.
(Ⅰ)求点
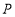 的坐标;
的坐标;(Ⅱ)求证:直线
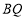 平行于抛物线的对称轴.
平行于抛物线的对称轴. -
科目: 来源: 题型:
查看答案和解析>>【题目】某校对高二年段的男生进行体检,现将高二男生的体重
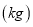 数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组
数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组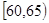 的人数为200.根据一般标准,高二男生体重超过
的人数为200.根据一般标准,高二男生体重超过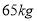 属于偏胖,低于
属于偏胖,低于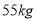 属于偏瘦.观察图形的信息,回答下列问题:
属于偏瘦.观察图形的信息,回答下列问题: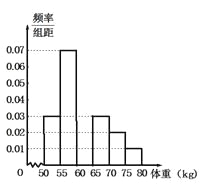
(1)求体重在
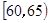 内的频率,并补全频率分布直方图;
内的频率,并补全频率分布直方图;(2)用分层抽样的方法从偏胖的学生中抽取
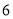 人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?(3)根据频率分布直方图,估计高二男生的体重的中位数与平均数.
相关试题

