【题目】已知圆M:x2+(y﹣2)2=r2(r>0)与曲线C:(y﹣2)(3x﹣4y+3)=0有三个不同的交点.
(1)求圆M的方程;
(2)已知点Q是x轴上的动点,QA,QB分别切圆M于A,B两点. ①若 ![]() ,求|MQ|及直线MQ的方程;
,求|MQ|及直线MQ的方程;
②求证:直线AB恒过定点.
参考答案:
【答案】
(1)解:因为直线3x﹣4y+3=0与圆M相切,
故圆心(0,2)到直线的距离为r,即: ![]() ,r=1.
,r=1.
所以圆的方程为x2+(y﹣2)2=1.
(2)解:①设直线MQ,AB交于点P,则 ![]() ,
,
又|AM|=1,所以 ![]() ,
,
而|AM|2=|MP||MQ|,所以|MQ|=3,
设Q(x0,0),而点M(0,2),由 ![]() ,
, ![]() ,
,
则 ![]() 或
或 ![]() ,
,
从而直线MQ的方程为: ![]() 或
或 ![]() .
.
②证明:设点Q(q,0),由几何性质可以知道,A,B在以MQ为直径的圆上,
此圆的方程为x2+y2﹣qx﹣2y=0,AB为两圆的公共弦,
两圆方程相减得qx﹣2y+3=0,
即 ![]() ,
,
所以过定点 ![]() .
.
【解析】(1)因为直线3x﹣4y+3=0与圆M相切,圆心(0,2)到直线的距离为r,即可求圆M的方程;(2)①|AM|2=|MP||MQ|,所以|MQ|=3,求出Q的坐标,即可求出直线MQ的方程;②求出直线AB的方程,即可证明直线AB恒过定点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l的斜率为k,经过点(1,﹣1),将直线向右平移3个单位,再向上平移2个单位,得到直线m,若直线m不经过第四象限,则直线l的斜率k的取值范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以原点为极点,
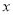 轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线
轴的正半轴为极轴,以相同的长度单位建立极坐标系,已知直线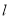 的极坐标方程为
的极坐标方程为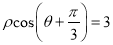 ,曲线
,曲线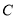 的极坐标方程为
的极坐标方程为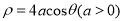 .
.(1)设
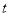 为参数,若
为参数,若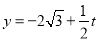 ,求直线
,求直线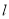 的参数方程;
的参数方程;(2)已知直线
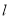 与曲线
与曲线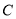 交于
交于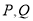 ,设
,设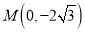 ,且
,且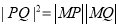 ,求实数
,求实数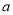 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果,在
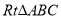 中,
中, 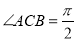 ,
, 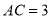 ,
, 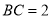 ,
, 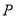 是
是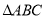 内的一点.
内的一点.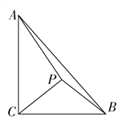
(1)若
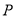 是等腰直角三角形
是等腰直角三角形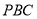 的直角顶点,求
的直角顶点,求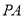 的长;
的长;(2)若
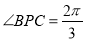 ,设
,设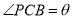 ,求
,求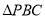 的面积
的面积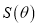 的解析式,并求
的解析式,并求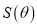 的最大值.
的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】一商场在某日促销活动中,对9时至14时的销售额进行统计,其频率分布直方图如图所示,已知9时至10时的销售额为2.5万元,则11时至12时的销售为( )
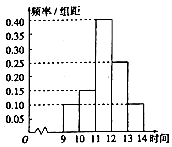
A.100万元
B.10万元
C.7.5万元
D.6.25万元 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 是梯形,四边形
是梯形,四边形 是矩形,且平面
是矩形,且平面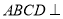 平面
平面 ,
,  ,
,  ,
,  ,
,  是线段
是线段 上的动点.
上的动点.
(1)试确定点
 的位置,使
的位置,使 平面
平面 ,并说明理由;
,并说明理由;(2)在(1)的条件下,求平面
 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 =
= 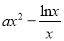 ,
, 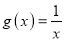 .
.(1)若函数
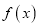 在
在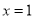 处取得极值,求
处取得极值,求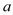 的值,并判断
的值,并判断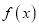 在
在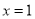 处取得极大值还是极小值.
处取得极大值还是极小值.(2)若
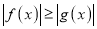 在
在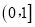 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
相关试题

