【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 20 | 40 | 80 | 50 | 10 | |
男性用户 | 分值区间 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
频数 | 45 | 75 | 90 | 60 | 30 |
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望.
参考答案:
【答案】
(1)解:女性用户和男性用户的频率分布直方图分别如下左、右图:
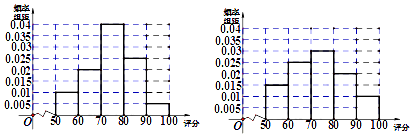
由图可得女性用户的波动小,男性用户的波动大
(2)解:运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,
其中评分小于90分的人数为4,从6人人任取3人,
记评分小于90分的人数为X,则X取值为1,2,3,
![]() ,
,
![]() ,
,
![]() .
.
所以X的分布列为
X | 1 | 2 | 3 |
P |
|
|
|
![]() 或
或 ![]()
【解析】(Ⅰ)求出女性用户和男性用户的频率分布直方图,由图可得女性用户的波动小,男性用户的波动大.(Ⅱ)运用分层抽样从男性用户中抽取20名用户,评分不低于80分有6人,其中评分小于90分的人数为4,从6人人任取3人,记评分小于90分的人数为X,则X取值为1,2,3,分别求出相应在的概率,由此能求出X的分布列和数学期望.
【考点精析】掌握离散型随机变量及其分布列是解答本题的根本,需要知道在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC的三个内角A,B,C所对应的边分别为a,b,c,且满足bcosC+
 c=a.
c=a.
(1)求△ABC的内角B的大小;
(2)若△ABC的面积S=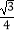 b2 , 试判断△ABC的形状.
b2 , 试判断△ABC的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,直线
,直线 ,
, .
.(1)求证:对
 ,直线
,直线 与圆
与圆 总有两个不同的交点
总有两个不同的交点 ;
;(2)是否存在实数
 ,使得圆
,使得圆 上有四点到直线
上有四点到直线 的距离为
的距离为 ?若存在,求出
?若存在,求出 的范围;若不存在,说明理由;
的范围;若不存在,说明理由;(3)求弦
 的中点
的中点 的轨迹方程,并说明其轨迹是什么曲线.
的轨迹方程,并说明其轨迹是什么曲线. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列{an}的首项a1=1,且(n+1)a
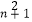 +anan+1﹣na
+anan+1﹣na  =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;、
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
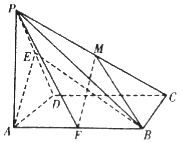
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 在区间
在区间 上有最大值4和最小值1.设
上有最大值4和最小值1.设 .
.(1)求
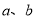 的值;
的值;(2)若不等式
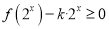 在
在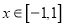 上有解,求实数
上有解,求实数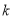 的取值范围;
的取值范围;(3)若
 有三个不同的实数解,求实数
有三个不同的实数解,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P是长轴长为
 的椭圆Q:
的椭圆Q: 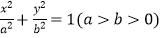 上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为
上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为  .
.
(1)求椭圆Q的方程;
(2)设过左焦点F1且不与坐标轴垂直的直线l交椭圆于C,D两点,线段CD的垂直平分线与x轴交于点G,点G横坐标的取值范围是 ,求|CD|的最小值.
,求|CD|的最小值.
相关试题

