搜索
【题目】已知△ABC的三个内角A，B，C所对应的边分别为a，b，c，且满足bcosC+ 
c=a．
（1）求△ABC的内角B的大小；
（2）若△ABC的面积S= 
b2 ， 试判断△ABC的形状．
参考答案：
【答案】
（1）解：∵bcosC+ 
c=a．
由正弦定理，可得sinBcosC 
sinC=sinA．
∵sinA=sin（B+C）．
∴sinBcosC+ sinC=sinBcosC+sinCcosB
∵0＜C＜π，sinC≠0．
∴cosB= ．
∵0＜B＜π，
∴B= 
．
（2）解：由△ABC的面积S= 
b2= acsinB，
可得：b2=ac．
由余弦定理：cosB= = 
，
得：a2+c2﹣2ac=0，即（a﹣c）2=0．
∴a=c．
故得△ABC是等腰三角形．
【解析】先利用正弦定理将边转化为角，再利用两角和的正弦公式可得cosB，进而可得角B的大小；（2）先利用三角形的面积公式可得b2=ac，再利用余弦定理可得a=c，从而可得△ABC的形状．
-
科目： 来源： 题型：
查看答案和解析>>【题目】设函数f（x）=
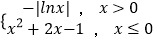，若f（a）=f（b）=f（c）=f（d），其中a，b，c，d互不相等，则对于命题p：abcd∈（0，1）和命题q：a+b+c+d∈[e+e﹣1﹣2，e2+e﹣2﹣2）真假的判断，正确的是（ ）
A.p假q真
B.p假q假
C.p真q真
D.p真q假 -
科目： 来源： 题型：
查看答案和解析>>【题目】若函数h（x）=ax3+bx2+cx+d（a≠0）图象的对称中心为M（x0 ， h（x0）），记函数h（x）的导函数为g（x），则有g′（x0）=0，设函数f（x）=x3﹣3x2+2，则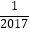f（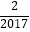
）+f（ 
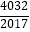）+…+f（ 
）+f（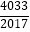 
）= ． -
科目： 来源： 题型：
查看答案和解析>>【题目】已知数列
满足
，且
.（Ⅰ）证明：数列
为等差数列，并求数列的通项公式；（Ⅱ）若记
为满足不等式
的正整数
的个数，设
，求数列
的最大项与最小项的值.【答案】(1)见解析;(2)最大项为
，最小项为
.【解析】试题分析：（Ⅰ）对
两边取倒数，移项即可得出
，故而数列为等差数列，利用等差数列的通项公式求出
，从而可得出
；（Ⅱ）根据不等式
，，得
，又
，从而
，当
为奇数时，
单调递减，
；当为偶数时单调递增，
综上的最大项为，最小项为
.试题解析：（Ⅰ）由于
，
，则
∴
，则
，即
为常数 又
，∴数列是以1为首项，
为公比的等比数列从而
，即
.（Ⅱ）由
即
，得，又
，从而故
当
为奇数时，
，单调递减，；当
为偶数时，
，单调递增，综上
的最大项为，最小项为.【题型】解答题
【结束】
22【题目】已知向量
，
，若函数
的最小正周期为
，且在区间
上单调递减.（Ⅰ）求
的解析式；（Ⅱ）若关于
的方程
在
有实数解，求
的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知圆
，直线
，
.（1）求证：对
，直线
与圆
总有两个不同的交点
；（2）是否存在实数
，使得圆上有四点到直线的距离为
？若存在，求出的范围；若不存在，说明理由；（3）求弦
的中点
的轨迹方程，并说明其轨迹是什么曲线. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知正项数列{an}的首项a1=1，且（n+1）a
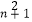+anan+1﹣na 
=0对n∈N*都成立．
（1）求{an}的通项公式；、
（2）记bn=a2n﹣1a2n+1 ， 数列{bn}的前n项和为Tn ， 证明：Tn＜
． -
科目： 来源： 题型：
查看答案和解析>>【题目】某手机厂商推出一次智能手机，现对500名该手机使用者（200名女性，300名男性）进行调查，对手机进行打分，打分的频数分布表如下：
女性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100）
频数
20
40
80
50
10
男性用户
分值区间
[50，60）
[60，70）
[70，80）
[80，90）
[90，100）
频数
45
75
90
60
30
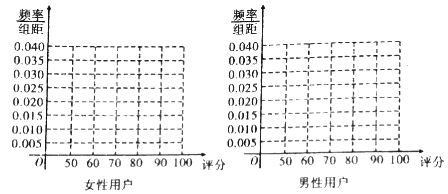
（1）完成下列频率分布直方图，并比较女性用户和男性用户评分的方差大小（不计算具体值，给出结论即可）；
（2）根据评分的不同，运用分层抽样从男性用户中抽取20名用户，在这20名用户中，从评分不低于80分的用户中任意取3名用户，求3名用户评分小于90分的人数的分布列和期望．
相关试题
