【题目】已知函数![]() 在区间
在区间![]() 上有最大值4和最小值1.设
上有最大值4和最小值1.设![]() .
.
(1)求![]() 的值;
的值;
(2)若不等式![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若![]() 有三个不同的实数解,求实数
有三个不同的实数解,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】试题分析:(1)由函数![]() ,
, ![]() 在区间
在区间![]() 上是增函数,故
上是增函数,故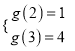 ,由此解得
,由此解得![]() 的值;(2)不等式化为
的值;(2)不等式化为![]() ,故有
,故有![]() ,求出
,求出![]() 的最小值,从而求得
的最小值,从而求得![]() 的取值范围;(3)方程,令
的取值范围;(3)方程,令![]() ,原方程等价于
,原方程等价于![]() ,构造函数
,构造函数![]() ,通过数形结合与等价转化的思想可求得
,通过数形结合与等价转化的思想可求得![]() 的范围.
的范围.
试题解析:(1)![]() ,
,
因为![]() ,所以
,所以![]() 在区间
在区间![]() 上是增函数,故
上是增函数,故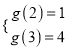 ,解得
,解得![]() ,
,
(2)由已知可得![]() ,
,
所以![]() 可化为
可化为![]() ,
,
化为![]() ,令
,令![]() ,则
,则![]() ,因
,因![]() ,故
,故![]() ,
,
记![]() ,因为
,因为![]() ,故
,故![]() ,所以
,所以![]() 得取值范围是
得取值范围是![]() .
.
(3)原方程可化为![]()
令![]() ,则
,则![]() ,
, ![]() 有两个不同的实数解
有两个不同的实数解![]() ,
,
其中![]() ,或
,或![]() .
.
记![]() ,则
,则![]() ① 或
① 或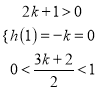 ②
②
解不等组①,得![]() ,而不等式组②无实数解,所以实数
,而不等式组②无实数解,所以实数![]() 的取值范围是
的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正项数列{an}的首项a1=1,且(n+1)a
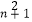 +anan+1﹣na
+anan+1﹣na  =0对n∈N*都成立.
=0对n∈N*都成立.
(1)求{an}的通项公式;、
(2)记bn=a2n﹣1a2n+1 , 数列{bn}的前n项和为Tn , 证明:Tn< .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】某手机厂商推出一次智能手机,现对500名该手机使用者(200名女性,300名男性)进行调查,对手机进行打分,打分的频数分布表如下:
女性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100)
频数
20
40
80
50
10
男性用户
分值区间
[50,60)
[60,70)
[70,80)
[80,90)
[90,100)
频数
45
75
90
60
30
(1)完成下列频率分布直方图,并比较女性用户和男性用户评分的方差大小(不计算具体值,给出结论即可);
(2)根据评分的不同,运用分层抽样从男性用户中抽取20名用户,在这20名用户中,从评分不低于80分的用户中任意取3名用户,求3名用户评分小于90分的人数的分布列和期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,PA⊥底面ABCD,AD=AP,E为棱PD中点.
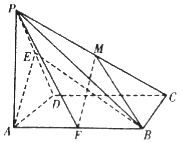
(1)求证:PD⊥平面ABE;
(2)若F为AB中点, ,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-
,试确定λ的值,使二面角P﹣FM﹣B的余弦值为-  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P是长轴长为
 的椭圆Q:
的椭圆Q: 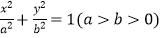 上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为
上异于顶点的一个动点,O为坐标原点,A为椭圆的右顶点,点M为线段PA的中点,且直线PA与OM的斜率之积恒为  .
.
(1)求椭圆Q的方程;
(2)设过左焦点F1且不与坐标轴垂直的直线l交椭圆于C,D两点,线段CD的垂直平分线与x轴交于点G,点G横坐标的取值范围是 ,求|CD|的最小值.
,求|CD|的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,已知△ABC三个顶点坐标为A(7,8),B(10,4),C(2,-4).
(1)求BC边上的中线所在直线的方程;
(2)求BC边上的高所在直线的方程.
【答案】(1)
 ;(2)
;(2)
【解析】试题分析:(1)根据中点坐标公式求出
 中点
中点 的坐标,根据斜率公式可求得
的坐标,根据斜率公式可求得 的斜率,利用点斜式可求
的斜率,利用点斜式可求 边上的中线所在直线的方程;(2)先根据斜率公式求出
边上的中线所在直线的方程;(2)先根据斜率公式求出 的斜率,从而求出
的斜率,从而求出 边上的高所在直线的斜率为
边上的高所在直线的斜率为 ,利用点斜式可求
,利用点斜式可求 边上的高所在直线的方程.
边上的高所在直线的方程.试题解析:(1)由B(10,4),C(2,-4),得BC中点D的坐标为(6,0),
所以AD的斜率为k=
 =8,
=8, 所以BC边上的中线AD所在直线的方程为y-0=8(x-6),
即8x-y-48=0.
(2)由B(10,4),C(2,-4),得BC所在直线的斜率为k=
 =1,
=1, 所以BC边上的高所在直线的斜率为-1,
所以BC边上的高所在直线的方程为y-8=-(x-7),即x+y-15=0.
【题型】解答题
【结束】
17【题目】已知直线l:x-2y+2m-2=0.
(1)求过点(2,3)且与直线l垂直的直线的方程;
(2)若直线l与两坐标轴所围成的三角形的面积大于4,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】第35届牡丹花会期间,我班有5名学生参加志愿者服务,服务场所是王城公园和牡丹公园.
(1)若学生甲和乙必须在同一个公园,且甲和丙不能在同一个公园,则共有多少种不同的分配方案?
(2)每名学生都被随机分配到其中的一个公园,设X,Y分别表示5名学生分配到王城公园和牡丹公园的人数,记ξ=|X﹣Y|,求随机变量ξ的分布列和数学期望E(ξ)
相关试题

