【题目】某二手交易市场对某型号的二手汽车的使用年数![]() (
(![]() )与销售价格
)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
销售价格 | 16 | 13 | 9.5 | 7 | 4.5 |
(I)试求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() .
.
(参考公式: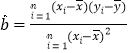 ,
,![]() )
)
(II)已知每辆该型号汽车的收购价格为![]() 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测![]() 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润![]() 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格)
参考答案:
【答案】(I)![]() .
.
(II)当![]() 时,利润
时,利润![]() 取得最大值.
取得最大值.
【解析】分析:(I)由题意可求得![]() ,结合所给公式可得
,结合所给公式可得![]() ,从而可得线性回归方程.(II)由题意可得
,从而可得线性回归方程.(II)由题意可得![]() ,根据二次函数的知识求得最值即可.
,根据二次函数的知识求得最值即可.
详解:(I)由表中数据得
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
∴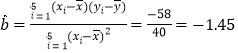 ,
,
∴![]() ,
,
∴![]() 关于
关于![]() 的回归直线方程为
的回归直线方程为![]() .
.
(II)根据题意得利润
![]()
∴当![]() 时,利润
时,利润![]() 取得最大值.
取得最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只蚂蚁在边长分别为3,4,5的三角形区域内随机爬行,则其恰在离三个顶点距离都大于1的地方的概率为( )
A.
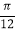 B.
B. 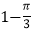 C.
C. 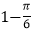 D.
D. 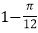
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240,160,160.现采用分层抽样的方法从中抽取7名同学去某敬老院参加献爱心活动.
(Ⅰ)应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人?
(Ⅱ)设抽出的7名同学分别用A,B,C,D,E,F,G表示,现从中随机抽取2名同学承担敬老院的卫生工作.
(i)试用所给字母列举出所有可能的抽取结果;
(ii)设M为事件“抽取的2名同学来自同一年级”,求事件M发生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
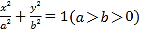 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为 ,
, .
.(1)求椭圆的方程;
(2)设直线
 与椭圆交于
与椭圆交于 ,
, 两点,
两点, 与直线
与直线 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若 的面积是
的面积是 面积的2倍,求
面积的2倍,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在三棱锥
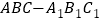 中,底面为正三角形,侧棱垂直于底面,
中,底面为正三角形,侧棱垂直于底面,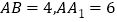 .若
.若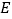 是棱
是棱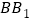 上的点,且
上的点,且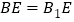 ,则异面直线
,则异面直线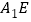 与
与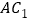 所成角的余弦值为( )
所成角的余弦值为( )
A.
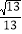 B.
B. 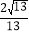 C.
C. 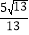 D.
D. 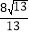
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲乙两辆车去同一货场装货物,货场每次只能给一辆车装货物,所以若两辆车同时到达,则需要有一车等待.已知甲、乙两车装货物需要的时间都为20分钟,倘若甲、乙两车都在某1小时内到达该货场,则至少有一辆车需要等待装货物的概率是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

