搜索
【题目】一只蚂蚁在边长分别为3,4,5的三角形区域内随机爬行,则其恰在离三个顶点距离都大于1的地方的概率为( )
A. 
B. 
C. 
D. 
参考答案：
【答案】D
【解析】
离三个顶点距离正好等于1的地方是分别以三个顶点为圆心，1为半径的圆弧，所以离三个顶点距离都大于1的地方为该三角形内，分别以三个顶点为顶点，1为半径的扇形区域以外的部分，则蚂蚁在该区域的概率为该区域的面积比三角形区域面积
因为三角形区域边长分别为3,4,5，所以该三角形为直角三角形，面积为
，离三个顶点距离正好等于1的地方是分别以三个顶点为圆心，1为半径的圆弧，所以离三个顶点距离都大于1的地方为该三角形内，分别以三个顶点为顶点，1为半径的扇形区域以外的部分，三个扇形的顶角和为
，所以三个扇形面积和为
，所以蚂蚁在该区域的概率为
，选择D项
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
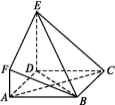
(1)求二面角F-BE-D的余弦值;
(2)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆C的中心在原点，离心率等于
，它的一个短轴端点恰好是抛物线
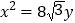的焦点．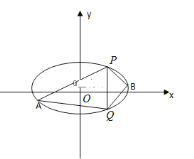
（1）求椭圆C的方程；
（2）已知P（2，3）、Q（2，﹣3）是椭圆上的两点，A，B是椭圆上位于直线PQ两侧的动点，若直线AB的斜率为
，求四边形APBQ面积的最大值； -
科目： 来源： 题型：
查看答案和解析>>【题目】已知椭圆
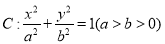经过点M（﹣2，﹣1），离心率为
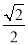．过点M作倾斜角互补的两条直线分别与椭圆C交于异于M的另外两点P、Q．(Ⅰ)求椭圆C的方程；
（Ⅱ）试判断直线PQ的斜率是否为定值，证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知某校甲、乙、丙三个年级的学生志愿者人数分别为240，160，160．现采用分层抽样的方法从中抽取７名同学去某敬老院参加献爱心活动．
（Ⅰ）应从甲、乙、丙三个年级的学生志愿者中分别抽取多少人？
（Ⅱ）设抽出的7名同学分别用A，B，C，D，E，F，G表示，现从中随机抽取2名同学承担敬老院的卫生工作．
（i）试用所给字母列举出所有可能的抽取结果；
（ii）设M为事件“抽取的2名同学来自同一年级”，求事件M发生的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四棱锥P-ABCD中，AB//CD，且
（1）证明：平面PAB⊥平面PAD；
（2）若PA=PD=AB=DC,
,且四棱锥P-ABCD的体积为
，求该四棱锥的侧面积. -
科目： 来源： 题型：
查看答案和解析>>【题目】某二手交易市场对某型号的二手汽车的使用年数
（
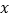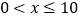）与销售价格
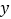（单位：万元/辆）进行整理，得到如下的对应数据：使用年数
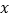
2
4
6
8
10
销售价格
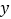
16
13
9.5
7
4.5
（I）试求
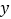关于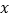的回归直线方程
.（参考公式：
，
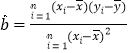）（II）已知每辆该型号汽车的收购价格为
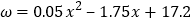万元，根据（I）中所求的回归方程，预测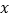为何值时，销售一辆该型号汽车所获得的利润
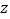最大？（利润=销售价格-收购价格）
相关试题
