【题目】如图,在三棱锥![]() 中,底面为正三角形,侧棱垂直于底面,
中,底面为正三角形,侧棱垂直于底面,![]() .若
.若![]() 是棱
是棱![]() 上的点,且
上的点,且![]() ,则异面直线
,则异面直线![]() 与
与![]() 所成角的余弦值为( )
所成角的余弦值为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
参考答案:
【答案】A
【解析】
以C为原点,CA为x轴,在平面ABC中过作AC的垂线为y轴,CC1为z轴,建立空间直角坐标系,利用向量法能求出异面直线A1E与![]() 所成角的余弦值.
所成角的余弦值.
以C为原点,CA为x轴,在平面ABC中过作AC的垂线为y轴,CC1为z轴,建立空间直角坐标系,
∵在三棱柱ABC﹣A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6,
E,F分别是棱BB1,CC1上的点,且BE=B1E,
∴A1(4,0,6),E(2,2![]() ,3),A(4,0,0),
,3),A(4,0,0),![]()
![]() (﹣2,2
(﹣2,2![]() ,﹣3),
,﹣3),![]() (-4,0,6),
(-4,0,6),
设异面直线![]() 与
与![]() 所成角所成角为θ,
所成角所成角为θ,
则cosθ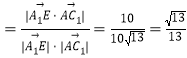 .
.
∴异面直线A1E与AF所成角的余弦值为![]() .
.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥P-ABCD中,AB//CD,且


(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC,
 ,且四棱锥P-ABCD的体积为
,且四棱锥P-ABCD的体积为 ,求该四棱锥的侧面积.
,求该四棱锥的侧面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】某二手交易市场对某型号的二手汽车的使用年数
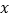 (
(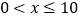 )与销售价格
)与销售价格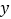 (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:使用年数
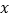
2
4
6
8
10
销售价格
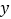
16
13
9.5
7
4.5
(I)试求
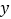 关于
关于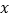 的回归直线方程
的回归直线方程 .
.(参考公式:
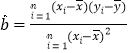 ,
, )
)(II)已知每辆该型号汽车的收购价格为
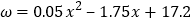 万元,根据(I)中所求的回归方程,预测
万元,根据(I)中所求的回归方程,预测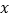 为何值时,销售一辆该型号汽车所获得的利润
为何值时,销售一辆该型号汽车所获得的利润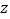 最大?(利润=销售价格-收购价格)
最大?(利润=销售价格-收购价格) -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
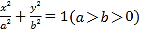 的右顶点为A,上顶点为B.已知椭圆的离心率为
的右顶点为A,上顶点为B.已知椭圆的离心率为 ,
, .
.(1)求椭圆的方程;
(2)设直线
 与椭圆交于
与椭圆交于 ,
, 两点,
两点, 与直线
与直线 交于点M,且点P,M均在第四象限.若
交于点M,且点P,M均在第四象限.若 的面积是
的面积是 面积的2倍,求
面积的2倍,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲乙两辆车去同一货场装货物,货场每次只能给一辆车装货物,所以若两辆车同时到达,则需要有一车等待.已知甲、乙两车装货物需要的时间都为20分钟,倘若甲、乙两车都在某1小时内到达该货场,则至少有一辆车需要等待装货物的概率是( )
A.
 B.
B.  C.
C.  D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】吸烟有害健康,远离烟草,珍惜生命。据统计一小时内吸烟5支诱发脑血管病的概率为0.02,一小时内吸烟10支诱发脑血管病的概率为0.16.已知某公司职员在某一小时内吸烟5支未诱发脑血管病,则他在这一小时内还能继吸烟5支不诱发脑血管病的概率为( )
A.
 B.
B. 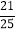 C.
C.  D. 不确定
D. 不确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直三棱柱
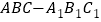 中,
中,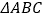 为等腰直角三角形,
为等腰直角三角形,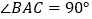 ,且
,且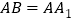 ,
,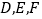 分别为
分别为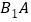 ,
,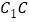 ,
,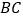 的中点.
的中点.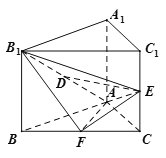
(1)求证:直线
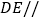 平面
平面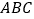 ;
;(2)求
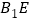 与平面
与平面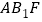 所成角的正弦值.
所成角的正弦值.
相关试题

