【题目】已知椭圆![]() 经过点
经过点![]() ,且离心率为
,且离心率为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设![]() 是椭圆上的点,直线
是椭圆上的点,直线![]() 与
与![]() (
(![]() 为坐标原点)的斜率之积为
为坐标原点)的斜率之积为![]() .若动点
.若动点![]() 满足
满足![]() ,试探究是否存在两个定点
,试探究是否存在两个定点![]() ,使得
,使得![]() 为定值?若存在,求
为定值?若存在,求![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
参考答案:
【答案】(Ⅰ)![]() ; (Ⅱ)见解析.
; (Ⅱ)见解析.
【解析】试题分析:(Ⅰ)利用椭圆的离心率计算公式和点在椭圆上列方程组求解即可得出.
(Ⅱ)利用向量的坐标运算、点在椭圆上满足椭圆的方程、斜率计算公式及其椭圆的定义即可得出.
试题解析:
(Ⅰ)∵![]() ∴
∴![]()
又∵椭圆![]() 经过点
经过点![]() ∴
∴![]()
解得:![]() ,
,![]()
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)设![]() ,
,![]() ,
,![]() ,则由
,则由![]() 得
得
即![]() ,
,![]() ,
,
因为点![]() 在椭圆
在椭圆![]() 上,
上,
所以![]() ,
,![]()
故![]()
![]()
![]()
![]()
![]()
设![]() ,
,![]() 分别为直线
分别为直线![]() 与
与![]() 的斜率,由题意知,
的斜率,由题意知,
![]() ,因此
,因此![]()
所以![]() ,
,
所以点![]() 是椭圆
是椭圆![]() 上的点,
上的点,
所以由椭圆的定义知存在点![]() ,满足
,满足![]() 为定值
为定值
又因为![]() ,
,
所以![]() 坐标分别为
坐标分别为![]() 、
、![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中国式过马路”是网友对部分中国人集体闯红灯现象的一种调侃,及“凑够一撮人就可以走了,和红绿灯无关”,某校研究性学习小组对全校学生按“跟从别人闯红灯”“从不闯红灯”“带头闯红灯”等三种形式进行调查获得下表数据:
跟从别人闯红灯
从不闯红灯
带头闯红灯
男生
980
410
60
女生
340
150
60
用分层抽样的方法,从所有被调查的人中抽取一个容量为
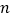 的样本,其中在“跟从别人闯红灯”的人中抽取了66人,
的样本,其中在“跟从别人闯红灯”的人中抽取了66人,(Ⅰ) 求
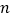 的值;
的值;(Ⅱ)在所抽取的“带头闯红灯”的人中,任选取2人参加星期天社区组织的“文明交通”宣传活动,求这2人中至少有1人是女生的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四棱锥
 中,底面
中,底面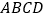 是直角梯形,
是直角梯形,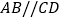 ,
,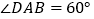 ,
,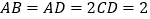 ,侧面
,侧面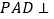 底面
底面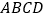 ,且
,且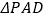 是以
是以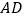 为底的等腰三角形.
为底的等腰三角形.(Ⅰ)证明:
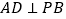
(Ⅱ)若四棱锥
 的体积等于
的体积等于 .问:是否存在过点
.问:是否存在过点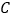 的平面
的平面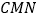 分别交
分别交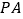 ,
,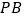 于点
于点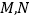 ,使得平面
,使得平面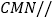 平面
平面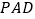 ?若存在,求出
?若存在,求出 的面积;若不存在,请说明理由.
的面积;若不存在,请说明理由.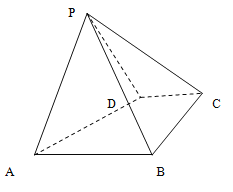
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,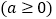 .
.(Ⅰ)若
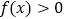 恒成立,求
恒成立,求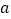 的取值范围;
的取值范围;(Ⅱ)设
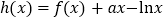 ,
,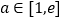 ,(
,(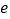 为自然对数的底数).是否存在常数
为自然对数的底数).是否存在常数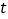 ,使
,使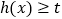 恒成立,若存在,求出
恒成立,若存在,求出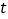 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知某中学高三文科班学生共有800人参加了数学与地理的水平测试,现从中随机抽取100人的数学与地理的水平测试成绩如下表:
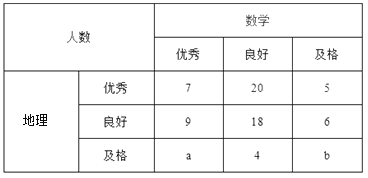
成绩分为优秀、良好、及格三个等级;横向,纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有
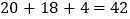 .
.(Ⅰ)若在该样本中,数学成绩优秀率是30%,求
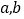 的值;
的值;(Ⅱ)已知
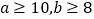 ,求数学成绩为优秀的人数比及格的人数少的概率.
,求数学成绩为优秀的人数比及格的人数少的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】线段AB的两端在直二面角α-l-β的两个面内,并与这两个面都成30°角,则异面直线AB与l所成的角是( )
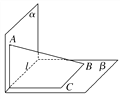
A. 30° B. 45°
C. 60° D. 75°
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
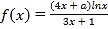 ,曲线
,曲线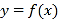 在点
在点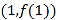 处的切线与直线
处的切线与直线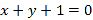 垂直.
垂直.(1)求
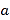 的值;
的值;(2)若对于任意的
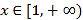 ,
, 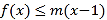 恒成立,求
恒成立,求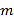 的取值范围;
的取值范围;(3)求证:
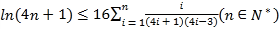 .
.
相关试题

