【题目】选修4-5:不等式选讲
设函数![]() .
.
(1)证明:![]() ;
;
(2)若不等式![]() 的解集是非空集,求
的解集是非空集,求![]() 的范围.
的范围.
参考答案:
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)直接计算![]() ,由绝对值不等式的性质及基本不等式证之即可;
,由绝对值不等式的性质及基本不等式证之即可;
(2)![]() ,分区间讨论去绝对值符号分别解不等式即可.
,分区间讨论去绝对值符号分别解不等式即可.
试题解析: (1)证明:函数f(x)=|x﹣a|,a<0,
则f(x)+f(﹣![]() )=|x﹣a|+|﹣
)=|x﹣a|+|﹣![]() ﹣a|=|x﹣a|+|
﹣a|=|x﹣a|+|![]() +a|≥|(x﹣a)+(
+a|≥|(x﹣a)+(![]() +a)|
+a)|
=|x+![]() |=|x|+
|=|x|+![]() ≥2
≥2![]() =2.
=2.
(2)f(x)+f(2x)=|x﹣a|+|2x﹣a|,a<0.
当x≤a时,f(x)=a﹣x+a﹣2x=2a﹣3x,则f(x)≥﹣a;
当a<x<![]() 时,f(x)=x﹣a+a﹣2x=﹣x,则﹣
时,f(x)=x﹣a+a﹣2x=﹣x,则﹣![]() <f(x)<﹣a;
<f(x)<﹣a;
当x![]() 时,f(x)=x﹣a+2x﹣a=3x﹣2a,则f(x)≥﹣
时,f(x)=x﹣a+2x﹣a=3x﹣2a,则f(x)≥﹣![]() .则f(x)的值域为[﹣
.则f(x)的值域为[﹣![]() ,+∞).
,+∞).
不等式f(x)+f(2x)<![]() 的解集非空,即为
的解集非空,即为![]() >﹣
>﹣![]() ,解得,a>﹣1,由于a<0,
,解得,a>﹣1,由于a<0,
则a的取值范围是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设
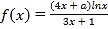 ,曲线
,曲线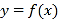 在点
在点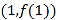 处的切线与直线
处的切线与直线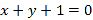 垂直.
垂直.(1)求
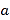 的值;
的值;(2)若对于任意的
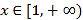 ,
, 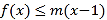 恒成立,求
恒成立,求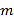 的取值范围;
的取值范围;(3)求证:
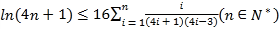 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】为响应市政府“绿色出行”的号召,王老师每个工作日上下班由自驾车改为选择乘坐地铁或骑共享单车这两种方式中的一种出行.根据王老师从2017年3月到2017年5月的出行情况统计可知,王老师每次出行乘坐地铁的概率是0.4,骑共享单车的概率是0.6.乘坐地铁单程所需的费用是3元,骑共享单车单程所需的费用是1元.记王老师在一个工作日内上下班所花费的总交通费用为X元,假设王老师上下班选择出行方式是相互独立的.
(I)求X的分布列和数学期望
 ;
;(II)已知王老师在2017年6月的所有工作日(按22个工作日计)中共花费交通费用110元,请判断王老师6月份的出行规律是否发生明显变化,并依据以下原则说明理由.
原则:设
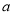 表示王老师某月每个工作日出行的平均费用,若
表示王老师某月每个工作日出行的平均费用,若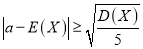 ,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注:
,则有95%的把握认为王老师该月的出行规律与前几个月的出行规律相比有明显变化.(注:  )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
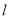 与圆C:
与圆C: 相交于A,B两点,弦AB中点为M(0,1),
相交于A,B两点,弦AB中点为M(0,1),(1)求实数
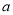 的取值范围以及直线
的取值范围以及直线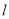 的方程;
的方程;(2)若圆C上存在四个点到直线
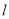 的距离为
的距离为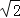 ,求实数a的取值范围;
,求实数a的取值范围;(3)已知N(0,﹣3),若圆C上存在两个不同的点P,使
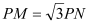 ,求实数
,求实数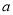 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】四棱锥P﹣ABCD中,底面ABCD是边长为8的菱形,∠BAD=
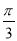 ,若PA=PD=5,平面PAD⊥平面ABCD.
,若PA=PD=5,平面PAD⊥平面ABCD.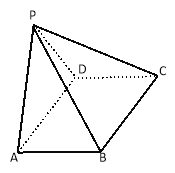
(1)求四棱锥P﹣ABCD的体积;
(2)求证:AD⊥PB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD为平行四边形,四边形ADEF是正方形,且BD⊥平面CDE,H是BE的中点,G是AE,DF的交点.

(1)求证:GH∥平面CDE;
(2)求证:面ADEF⊥面ABCD.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经营一批进价为
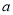 元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:
元/台的小商品,经调查得知如下数据.若销售价上下调整,销售量和利润大体如下:销售价(
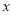 元/台)
元/台)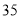
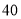
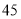
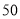
日销售量(
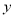 台)
台)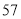
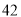
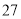
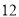
日销售额(
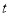 元)
元)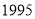
日销售利润(
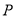 元)
元)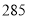
(1)在下面给出的直角坐标系中,根据表中的数据描出实数对
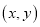 的对应点,并写出
的对应点,并写出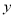 与
与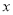 的一个函数关系式;
的一个函数关系式;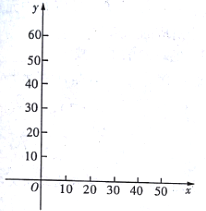
(2)请把表中的空格里的数据填上;
(3)根据表中的数据求
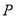 与
与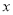 的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
的函数关系式,并指出当销售单价为多少元时,才能获得最大日销售利润?
相关试题

