搜索
【题目】如图，正方体的底面与正四面体的底面在同一平面α上，且AB∥CD，正方体的六个面所在的平面与直线CE，EF相交的平面个数分别记为m，n，那么m+n=（ ） 
A.8
B.9
C.10
D.11
参考答案：
【答案】A
【解析】解：由题意可知直线CE与正方体的上底面平行在正方体的下底面上，与正方体的四个侧面不平行，所以m=4，
直线EF与正方体的左右两个侧面平行，与正方体的上下底面相交，前后侧面相交，所以n=4，所以m+n=8．
故选A．
【考点精析】解答此题的关键在于理解平面的基本性质及推论的相关知识，掌握如果一条直线上的两点在一个平面内，那么这条直线在此平面内;过不在一条直线上的三点，有且只有一个平面;如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知过点
的椭圆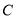
： 
（
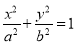）的左右焦点分别为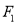
、
， 
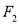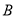为椭圆上的任意一点，且
， 
， 
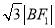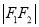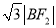成等差数列.（1）求椭圆
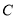的标准方程；（2）直线
： 
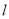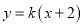交椭圆于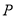
， 
两点，若点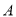
始终在以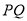
为直径的圆外，求实数
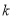的取值范围. -
科目： 来源： 题型：
查看答案和解析>>【题目】已知函数
．（1）当
时，若函数
恰有一个零点，求实数
的取值范围；（2）当
， 
时，对任意
，有
成立，求实数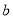
的取值范围． -
科目： 来源： 题型：
查看答案和解析>>【题目】阅读如下程序框图，如果输出i=5，那么在空白矩形框中应填入的语句为（ ）
A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4 -
科目： 来源： 题型：
查看答案和解析>>【题目】为了更好地规划进货的数量，保证蔬菜的新鲜程度，某蔬菜商店从某一年的销售数据中，随机抽取了8组数据作为研究对象，如表所示（
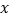（吨）为买进蔬菜的数量，
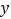（天）为销售天数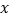）：2
3
4
5
6
7
9
12
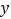
1
2
3
3
4
5
6
8
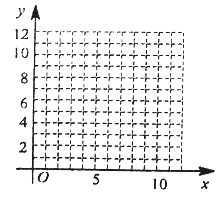
（1）根据上表数据在所给坐标系中绘制散点图，并用最小二乘法求出
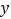关于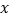的线性回归方程
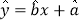；（2）根据（Ⅰ）中的计算结果，该蔬菜商店准备一次性买进25吨，预计需要销售多少天？
（参考数据和公式：
，
，
，
，
，
.） -
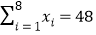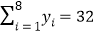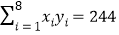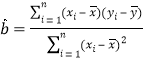
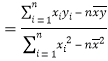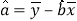科目： 来源： 题型：
查看答案和解析>>【题目】在平面直角坐标系
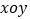中，已知任意角
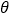以坐标原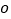点
为顶点，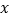
轴的非负半轴为始边，若终边经过点
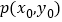，且
，定义：
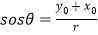，称“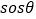
”为“正余弦函数”，对于“正余弦函数
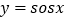”，有同学得到以下性质：①该函数的值域为
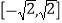； ②该函数的图象关于原点对称；③该函数的图象关于直线
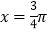对称； ④该函数为周期函数，且最小正周期为
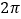；⑤该函数的递增区间为
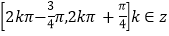.其中正确的是__________．（填上所有正确性质的序号）
-
科目： 来源： 题型：
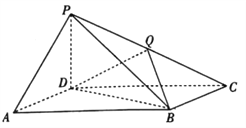
查看答案和解析>>【题目】如图，在四棱锥
中，底面
为平行四边形， 
， 
，且
底面
.
（1）证明：平面
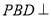平面
；（2）若
为
的中点，且
，求二面角
的大小.
相关试题
