【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为平行四边形,
为平行四边形, ![]() ,
, ![]() ,且
,且![]() 底面
底面![]() .
.
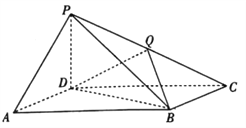
(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() 为
为![]() 的中点,且
的中点,且![]() ,求二面角
,求二面角![]() 的大小.
的大小.
参考答案:
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)易证得![]() ,
, ![]() ,所以有
,所以有![]() 平面
平面![]() ,从而得证;
,从而得证;
(2)分别以![]() ,
, ![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,分别求得平面
,分别求得平面![]() 的法向量为
的法向量为![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,由法向量的所成角可得解.
,由法向量的所成角可得解.
试题解析:
(1)证明:∵![]() ,∴
,∴![]() ,
,
∴![]() ,∴
,∴![]() .
.
又∵![]() 底面
底面![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
而![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() .
.
(2)解:由(1)知, ![]() 平面
平面![]() ,
,
分别以![]() ,
, ![]() ,
, ![]() 为
为![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴建立空间直角坐标系
轴建立空间直角坐标系![]() ,如图所示,设
,如图所示,设![]() ,则
,则![]() ,令
,令![]() ,则
,则![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,  ,
,
∴![]() ,
,  .
.
∴![]() ,∴
,∴![]() .
.
故 ,
,  .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
则![]() ,即
,即 ,
,
令![]() ,得
,得![]() .
.
易知平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则![]() ,
,
∴二面角![]() 的大小为
的大小为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )

A.8
B.9
C.10
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如表所示(
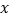 (吨)为买进蔬菜的数量,
(吨)为买进蔬菜的数量,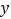 (天)为销售天数):
(天)为销售天数):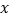
2
3
4
5
6
7
9
12
1
2
3
3
4
5
6
8
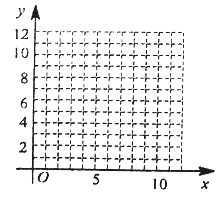
(1)根据上表数据在所给坐标系中绘制散点图,并用最小二乘法求出
 关于
关于 的线性回归方程
的线性回归方程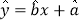 ;
;(2)根据(Ⅰ)中的计算结果,该蔬菜商店准备一次性买进25吨,预计需要销售多少天?
(参考数据和公式:
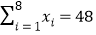 ,
,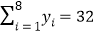 ,
,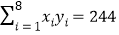 ,
, ,
,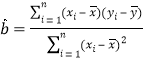
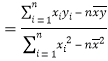 ,
,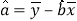 .)
.) -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,已知任意角
中,已知任意角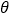 以坐标原点
以坐标原点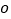 为顶点,
为顶点,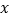 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点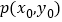 ,且
,且 ,定义:
,定义: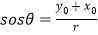 ,称“
,称“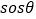 ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数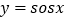 ”,有同学得到以下性质:
”,有同学得到以下性质:①该函数的值域为
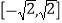 ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;③该函数的图象关于直线
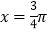 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为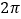 ;
;⑤该函数的递增区间为
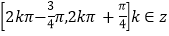 .
.其中正确的是__________.(填上所有正确性质的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】过点(
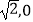 )引直线l与曲线y=
)引直线l与曲线y= 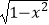 相交于A,B两点,O为坐标原点,当△ABO的面积取得最大值时,直线l的斜率等于( )
相交于A,B两点,O为坐标原点,当△ABO的面积取得最大值时,直线l的斜率等于( )
A.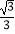
B.-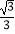
C.
D.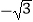
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1的半圆O与等边三角形ABC夹在两平行线l1 , l2之间,l∥l1 , l与半圆相交于F,G两点,与三角形ABC两边相交于E,D两点.设弧
 的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( )
的长为x(0<x<π),y=EB+BC+CD,若l从l1平行移动到l2 , 则函数y=f(x)的图象大致是( ) 
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业一天中不同时刻的用电量
 (万千瓦时)关于时间
(万千瓦时)关于时间 (单位:小时,其中
(单位:小时,其中 对应凌晨0点)的函数
对应凌晨0点)的函数 近似满足
近似满足
 ,如图是函数
,如图是函数 的部分图象.
的部分图象.
(1)求
 的解析式;
的解析式;(2)已知该企业某天前半日能分配到的供电量
 (万千瓦时)与时间
(万千瓦时)与时间 (小时)的关系可用线性函数模型
(小时)的关系可用线性函数模型 模拟,当供电量
模拟,当供电量 小于企业用电量
小于企业用电量 时,企业必须停产.初步预计开始停产的临界时间
时,企业必须停产.初步预计开始停产的临界时间 在中午11点到12点之间,用二分法估算
在中午11点到12点之间,用二分法估算 所在的一个区间(区间长度精确到15分钟).
所在的一个区间(区间长度精确到15分钟).
相关试题

