【题目】在平面直角坐标系![]() 中,已知任意角
中,已知任意角![]() 以坐标原点
以坐标原点![]() 为顶点,
为顶点,![]() 轴的非负半轴为始边,若终边经过点
轴的非负半轴为始边,若终边经过点![]() ,且
,且![]() ,定义:
,定义:![]() ,称“
,称“![]() ”为“正余弦函数”,对于“正余弦函数
”为“正余弦函数”,对于“正余弦函数![]() ”,有同学得到以下性质:
”,有同学得到以下性质:
①该函数的值域为![]() ; ②该函数的图象关于原点对称;
; ②该函数的图象关于原点对称;
③该函数的图象关于直线![]() 对称; ④该函数为周期函数,且最小正周期为
对称; ④该函数为周期函数,且最小正周期为![]() ;
;
⑤该函数的递增区间为![]() .
.
其中正确的是__________.(填上所有正确性质的序号)
参考答案:
【答案】①④⑤.
【解析】分析:根据“正余弦函数”的定义得到函数![]() ,然后根据三角函数的图象与性质分别进行判断即可得到结论.
,然后根据三角函数的图象与性质分别进行判断即可得到结论.
详解:①中,由三角函数的定义可知![]() ,
,
所以![]() ,所以是正确的;
,所以是正确的;
②中,![]() ,所以
,所以![]() ,所以函数关于原点对称是错位的;
,所以函数关于原点对称是错位的;
③中,当![]() 时,
时,![]() ,所以图象关于
,所以图象关于![]() 对称是错误的;
对称是错误的;
④中,![]() ,所以函数为周期函数,且最小正周期为
,所以函数为周期函数,且最小正周期为![]() ,所以是正确的;
,所以是正确的;
⑤中,因为![]() ,令
,令![]() ,
,
得![]() ,即函数的单调递增区间为
,即函数的单调递增区间为![]() ,所以是正确的,
,所以是正确的,
综上所述,正确命题的序号为①④⑤.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
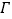 的两个焦点分别为
的两个焦点分别为 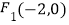 ,
, 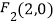 ,且经过点
,且经过点 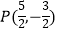 .
.
(Ⅰ)求椭圆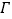 的标准方程;
的标准方程;
(Ⅱ)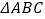 的顶点都在椭圆
的顶点都在椭圆 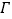 上,其中
上,其中 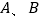 关于原点对称,试问
关于原点对称,试问  能否为正三角形?并说明理由.
能否为正三角形?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个正方体的平面展开图及该正方体的直观图的示意图如图所示.
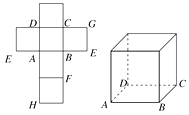
(1)请按字母F、G、H标记在正方体相应地顶点处(不需要说明理由);
(2)判断平面BEG与平面ACH的位置关系.并说明你的结论;
(3)证明:直线DF⊥平面BEG. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
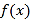 的图像是由函数
的图像是由函数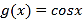 的图像经如下变换得到:先将
的图像经如下变换得到:先将 图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移
图像上所有点的纵坐标伸长到原来的2倍(横坐标不变),再将所得到的图像向右平移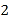 个单位长度.
个单位长度.(Ⅰ)求函数
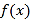 的解析式,并求其图像的对称轴方程;
的解析式,并求其图像的对称轴方程;(Ⅱ)已知关于
 的方程
的方程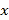 在
在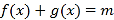 内有两个不同的解
内有两个不同的解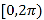 .
.(1)求实数m的取值范围;
(2)证明:
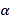
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知曲线C1:y=cos x,C2:y=sin (2x+
 ),则下面结论正确的是( )
),则下面结论正确的是( )A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移
 个单位长度,得到曲线C2
个单位长度,得到曲线C2B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移
 个单位长度,得到曲线C2
个单位长度,得到曲线C2C. 把C1上各点的横坐标缩短到原来的
 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2D. 把C1上各点的横坐标缩短到原来的
 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移 个单位长度,得到曲线C2
个单位长度,得到曲线C2 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
如图,在四棱锥P—ABCD中,侧面PAD⊥底面ABCD,侧棱PA=PD=
 ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.(Ⅰ)求证:PO⊥平面ABCD;
(Ⅱ)求异面直线PB与CD所成角的余弦值;
(Ⅲ)求点A到平面PCD的距离.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品在30天内每克的销售价格
 (元)与时间
(元)与时间 的函数图像是如图所示的两条线段
的函数图像是如图所示的两条线段 ,
, (不包含
(不包含 ,
, 两点);该商品在 30 天内日销售量
两点);该商品在 30 天内日销售量 (克)与时间
(克)与时间 (天)之间的函数关系如下表所示.
(天)之间的函数关系如下表所示.第
 天
天5
1
5
2
0
3
0
销售量
 克
克3
5
2
5
2
0
1
0

(1)根据提供的图象,写出该商品每克销售的价格
 (元)与时间
(元)与时间 的函数关系式;
的函数关系式;(2)根据表中数据写出一个反映日销售量
 随时间
随时间 变化的函数关系式;
变化的函数关系式;(3)在(2)的基础上求该商品的日销售金额的最大值,并求出对应的
 值.
值.(注:日销售金额=每克的销售价格×日销售量)
相关试题

