【题目】已知函数![]()
![]() .
.
(1)当![]() 时,若函数
时,若函数![]() 恰有一个零点,求实数
恰有一个零点,求实数![]() 的取值范围;
的取值范围;
(2)当![]() ,
, ![]() 时,对任意
时,对任意![]() ,有
,有![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
参考答案:
【答案】(1)![]() 或
或![]() (2)
(2)![]()
【解析】试题分析:(1)讨论![]() 、
、![]() 两种情况,分别利用导数研究函数的单调性,结合函数的单调性,利用零点存在定理可得函数
两种情况,分别利用导数研究函数的单调性,结合函数的单调性,利用零点存在定理可得函数![]() 恰有一个零点时实数
恰有一个零点时实数![]() 的取值范围;(2)对任意
的取值范围;(2)对任意![]() ,有
,有![]() 成立,等价于
成立,等价于![]() ,利用导数研究函数的单调性,分别求出最大值与最小值,解不等式即可的结果.
,利用导数研究函数的单调性,分别求出最大值与最小值,解不等式即可的结果.
试题解析:(1)函数![]() 的定义域为
的定义域为![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() .
.
①当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增,
上单调递增,
取![]() ,则
,则 ,
,
(或:因为![]() 且
且![]() 时,所以
时,所以![]() .)
.)
因为![]() ,所以
,所以![]() ,此时函数
,此时函数![]() 有一个零点.
有一个零点.
②当![]() 时,令
时,令![]() ,解得
,解得![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在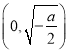 上单调递减;
上单调递减;
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在 上单调递增.
上单调递增.
要使函数![]() 有一个零点,则
有一个零点,则 即
即![]() .
.
综上所述,若函数![]() 恰有一个零点,则
恰有一个零点,则![]() 或
或![]() .
.
(2)因为对任意![]() ,有
,有![]() 成立,
成立,
因为![]() ,
,
所以![]() .
.
因为![]() ,则
,则![]() .
.
所以![]() ,所以
,所以![]() .
.
当![]() 时,
时, ![]() ,当
,当![]() 时,
时, ![]() ,
,
所以函数![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增, ![]() ,
,
因为![]() 与
与![]() ,所以
,所以![]() .
.
设![]()
![]() ,
,
则![]() .
.
所以![]() 在
在![]() 上单调递增,故
上单调递增,故![]() ,所以
,所以![]() .
.
从而![]()
![]() .
.
所以![]() 即
即![]() ,
,
设![]()
![]() ,则
,则![]() .
.
当![]() 时,
时, ![]() ,所以
,所以![]() 在
在![]() 上单调递增.
上单调递增.
又![]() ,所以
,所以![]() ,即为
,即为![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() 的取值范围为
的取值范围为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系xOy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1 , 直线C2的极坐标方程分别为ρ=4sinθ,ρcos(
 )=2
)=2  .
.
(1)求C1与C2交点的极坐标;
(2)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为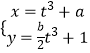 (t∈R为参数),求a,b的值.
(t∈R为参数),求a,b的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面斜坐标系
 中,
中, ,平面上任意一点
,平面上任意一点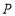 关于斜坐标系的斜坐标是这样定义的:若
关于斜坐标系的斜坐标是这样定义的:若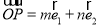 (其中
(其中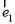 ,
,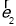 分别为与
分别为与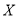 轴,
轴,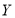 轴同方向的单位向量),则
轴同方向的单位向量),则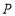 点的斜坐标为
点的斜坐标为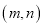

(1)若点
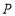 在斜坐标系
在斜坐标系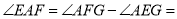 中的坐标为
中的坐标为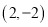 ,求点
,求点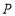 到原点
到原点 的距离.
的距离.(2)求以原点
 为圆心且半径为
为圆心且半径为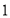 的圆在斜坐标系
的圆在斜坐标系 中的方程.
中的方程.(3)在斜坐标系
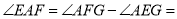 中,若直线
中,若直线 交(2)中的圆于
交(2)中的圆于 两点,则当
两点,则当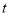 为何值时,
为何值时,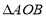 的面积取得最大值?并求此最大值.
的面积取得最大值?并求此最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知过点
 的椭圆
的椭圆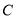 :
: 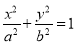 (
( )的左右焦点分别为
)的左右焦点分别为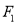 、
、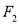 ,
, 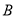 为椭圆上的任意一点,且
为椭圆上的任意一点,且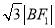 ,
, 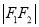 ,
, 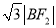 成等差数列.
成等差数列.(1)求椭圆
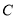 的标准方程;
的标准方程;(2)直线
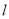 :
: 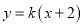 交椭圆于
交椭圆于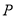 ,
,  两点,若点
两点,若点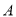 始终在以
始终在以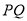 为直径的圆外,求实数
为直径的圆外,求实数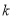 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读如下程序框图,如果输出i=5,那么在空白矩形框中应填入的语句为( )

A.S=2*i﹣2
B.S=2*i﹣1
C.S=2*I
D.S=2*i+4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方体的底面与正四面体的底面在同一平面α上,且AB∥CD,正方体的六个面所在的平面与直线CE,EF相交的平面个数分别记为m,n,那么m+n=( )

A.8
B.9
C.10
D.11 -
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好地规划进货的数量,保证蔬菜的新鲜程度,某蔬菜商店从某一年的销售数据中,随机抽取了8组数据作为研究对象,如表所示(
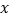 (吨)为买进蔬菜的数量,
(吨)为买进蔬菜的数量,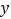 (天)为销售天数):
(天)为销售天数):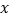
2
3
4
5
6
7
9
12
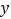
1
2
3
3
4
5
6
8
(1)根据上表数据在所给坐标系中绘制散点图,并用最小二乘法求出
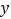 关于
关于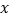 的线性回归方程
的线性回归方程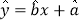 ;
;(2)根据(Ⅰ)中的计算结果,该蔬菜商店准备一次性买进25吨,预计需要销售多少天?
(参考数据和公式:
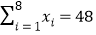 ,
,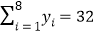 ,
,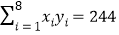 ,
, ,
,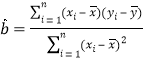
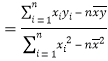 ,
,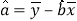 .)
.)
相关试题

