【题目】如图,三棱柱ABCA1B1C1的侧棱与底面垂直,AC=9,BC=12,AB=15,AA1=12,点D是AB的中点.
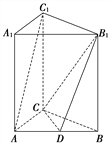
(1)求证:AC⊥B1C;
(2)求证:AC1∥平面CDB1.
参考答案:
【答案】详见解析
【解析】试题分析:(1)由C1C⊥平面ABC,得C1C⊥AC.再根据勾股定理得AC⊥BC. 利用线面垂直判定定理得AC⊥平面BCC1B1,即得AC⊥B1C.(2)连接BC1交B1C于O点,则由三角形中位线性质得OD∥AC1.再根据线面平行判定定理得结论
试题解析:(1)∵C1C⊥平面ABC,∴C1C⊥AC.
∵AC=9,BC=12,AB=15,
∴AC2+BC2=AB2,
∴AC⊥BC.
又BC∩C1C=C,∴AC⊥平面BCC1B1,
而B1C平面BCC1B1,
∴AC⊥B1C.
(2)连接BC1交B1C于O点,连接OD.如图,∵O,D分别为BC1,AB的中点,∴OD∥AC1.又OD平面CDB1,AC1平面CDB1.∴AC1∥平面CDB1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)全集U={2,4,-(a-3)2},集合A={2,a2-a+2},若UA={-1},求实数a的值. (2)已知A={x|2a≤x≤a+3},B={x|x<-1或x>5},若A∩B=,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=xln x-(x-1)(ax-a+1)(a∈R).
(1)若a=0,判断函数f(x)的单调性;
(2)若x>1时,f(x)<0恒成立,求a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
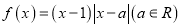 .
.(1)当
 时,求不等式
时,求不等式 的解集;
的解集;(2)当
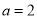 时,若对任意互不相等的实数
时,若对任意互不相等的实数 ,都有
,都有 成立,求实数
成立,求实数 的取值范围;
的取值范围;(3)判断函数
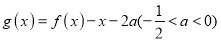 在
在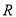 上的零点的个数,并说明理由.
上的零点的个数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某投资人欲将5百万元奖金投入甲、乙两种理财产品,根据银行预测,甲、乙两种理财产品的收益与投入奖金
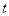 的关系式分别为
的关系式分别为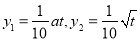 ,其中
,其中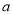 为常数且
为常数且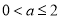 .设对乙种产品投入奖金
.设对乙种产品投入奖金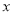 百万元,其中
百万元,其中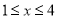 .
.(1)当
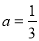 时,如何进行投资才能使得总收益
时,如何进行投资才能使得总收益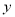 最大;(总收益
最大;(总收益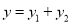 )
)(2)银行为了吸储,考虑到投资人的收益,无论投资人奖金如何分配,要使得总收益不低于
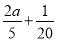 ,求
,求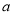 的取值范围.
的取值范围. -
科目: 来源: 题型:
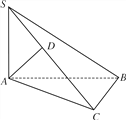
查看答案和解析>>【题目】如图所示,已知△ABC中,∠ACB=90°,SA⊥平面ABC,AD⊥SC,求证:AD⊥平面SBC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(1)从袋中随机取出两个球,求取出的球的编号之和不大于4的概率.
(2)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n,求n<m+2的概率.
相关试题

