【题目】已知函数f(x)=xln x-(x-1)(ax-a+1)(a∈R).
(1)若a=0,判断函数f(x)的单调性;
(2)若x>1时,f(x)<0恒成立,求a的取值范围.
参考答案:
【答案】见解析
【解析】(1)若a=0,f(x)=xln x-x+1,f′(x)=ln x.
∴当x∈(0,1)时,f′(x)<0,f(x)为减函数;
当x∈(1,+∞)时,f′(x)>0,f(x)为增函数.
(2)由题意知f(x)=xln x-(x-1)(ax-a+1)<0在(1,+∞)上恒成立.
①若a=0,则f(x)=xln x-x+1,f′(x)=ln x>0在x∈(1,+∞)上恒成立,∴f(x)为(1,+∞)上的增函数,∴f(x)>f(1)=0,即f(x)<0不成立.∴a=0不合题意.
②若a≠0,∵x>1,∴只需![]() =ln x-
=ln x-![]() <0在(1,+∞)上恒成立.
<0在(1,+∞)上恒成立.
记h(x)=ln x-![]() ,x∈(1,+∞),
,x∈(1,+∞),
则h′(x)=-![]() =-
=-![]() ,x∈(1,+∞).
,x∈(1,+∞).
由h′(x)=0,得x1=1,x2=![]() .
.
若a<0,则x2=![]() <1=x1,
<1=x1,
∴h′(x)>0在(1,+∞)上恒成立,故h(x)为增函数,
∴h(x)>h(1)=0,不合题意.
若0<a<![]() ,x∈
,x∈![]() 时,h′(x)>0,h(x)为增函数,
时,h′(x)>0,h(x)为增函数,
∴h(x)>h(1)=0,不合题意,
若a≥![]() ,x∈(1,+∞)时,h′(x)<0,h(x)为减函数,
,x∈(1,+∞)时,h′(x)<0,h(x)为减函数,
∴h(x)<h(1)=0,符合题意.
综上所述,若x>1时,f(x)<0恒成立,则a≥![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
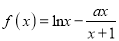 .
.(Ⅰ)若函数
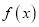 有极值,求实数
有极值,求实数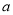 的取值范围;
的取值范围; (Ⅱ)当
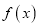 有两个极值点(记为
有两个极值点(记为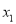 和
和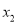 )时,求证:
)时,求证: 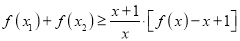 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
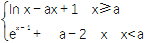 .(a>0)
.(a>0)(1)若a=1,证明:y=f(x)在R上单调递减;
(2)当a>1时,讨论f(x)零点的个数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司生产电饭煲,每年需投入固定成本40万元,每生产1万件还需另投入16万元的变动成本,设该公司一年内共生产电饭煲
 万件并全部销售完,每一万件的销售收入为
万件并全部销售完,每一万件的销售收入为 万元,且
万元,且 (
( ),该公司在电饭煲的生产中所获年利润为
),该公司在电饭煲的生产中所获年利润为 (万元),(注:利润=销售收入-成本)
(万元),(注:利润=销售收入-成本)(1)写出年利润
 (万元)关于年产量
(万元)关于年产量 (万件)的函数解析式,并求年利润的最大值;
(万件)的函数解析式,并求年利润的最大值;(2)为了让年利润
 不低于2360万元,求年产量
不低于2360万元,求年产量 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln x-ax(a∈R)(e=2.718 28…是自然对数的底数).
(1)判断f(x)的单调性;
(2)当f(x)<0在(0,+∞)上恒成立时,求a的取值范围;
(3)证明:当x∈(0,+∞)时,
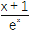 (1+x)
(1+x) 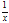 <e.
<e. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
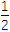 x2-2aln x+(a-2)x,a∈R.
x2-2aln x+(a-2)x,a∈R.(1)当a=1时,求函数f(x)的图象在点(1,f(1))处的切线方程.
(2)是否存在实数a,对任意的x1,x2∈(0,+∞)且x1≠x2有
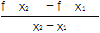 >a恒成立?若存在,求出a的取值范围;若不存在,说明理由.
>a恒成立?若存在,求出a的取值范围;若不存在,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 为公差不为零的等差数列,首项
为公差不为零的等差数列,首项 ,
,  的部分项
的部分项 、
、 、 、
、 、 恰为等比数列,且
恰为等比数列,且 ,
, ,
, .
.(1)求数列
 的通项公式
的通项公式 (用
(用 表示);
表示);(2)设数列
 的前
的前 项和为
项和为 , 求证:
, 求证:  (
( 是正整数
是正整数
相关试题

