【题目】如图,AB是⊙O的切线,ADE是⊙O的割线,AC=AB,连接CD,CE,分别与⊙O交于点F,点G. 
(1)求证:△ADC~△ACE;
(2)求证:FG∥AC.
参考答案:
【答案】
(1)证明:根据题意,可得:AB2=ADAE,
∵AC=AB,
∴AC2=ADAE,即 ![]() =
= ![]() ,
,
又∵∠CAD=∠EAC,
∴△ADC∽△ACE

(2)证明:∵F,G,E,D四点共圆,
∴∠CFG=∠AEC,
又∵∠ACF=∠AEC,
∴∠CFG=∠ACF,
∴FG∥AC
【解析】(1)根据已知和切割线定理可得AC2=ADAE,即 ![]() =
= ![]() ,又∠CAD=∠EAC,即可证明△ADC∽△ACE.(2)由F,G,E,D四点共圆,可得∠CFG=∠AEC,利用三角形相似可得∠ACF=∠AEC,通过证明∠CFG=∠ACF,即可得解FG∥AC.
,又∠CAD=∠EAC,即可证明△ADC∽△ACE.(2)由F,G,E,D四点共圆,可得∠CFG=∠AEC,利用三角形相似可得∠ACF=∠AEC,通过证明∠CFG=∠ACF,即可得解FG∥AC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆M::
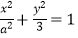 (a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(1)求椭圆方程;
(2)当直线l的倾斜角为45°时,求线段CD的长;
(3)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
如图,四棱锥
 的底面
的底面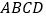 为菱形,
为菱形, 平面
平面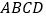 ,
, ,
, 分别为
分别为 的中点,
的中点, .
.
(Ⅰ)求证:平面
 平面
平面 .
.(Ⅱ)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln(x+a)+x2
(1)若当x=﹣1时,f(x)取得极值,求a的值,并讨论f(x)的单调性;
(2)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于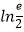 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,圆C的方程为
 (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(1)当m=3时,判断直线l与C的位置关系;
(2)当C上有且只有一点到直线l的距离等于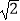 时,求C上到直线l距离为2
时,求C上到直线l距离为2 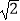 的点的坐标.
的点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知实数
 ,函数
,函数 .
.(1)当
 时,求
时,求 的最小值;
的最小值;(2)当
 时,判断
时,判断 的单调性,并说明理由;
的单调性,并说明理由;(3)求实数
 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数 ,都存在以
,都存在以 为边长的三角形.
为边长的三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:在△ABC中,若AB<BC,则sinC<sinA;命题q:已知a∈R,则“a>1”是“
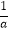 <1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
<1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
A.1
B.2
C.3
D.4
相关试题

