【题目】(本小题满分12分)
如图,四棱锥![]() 的底面
的底面![]() 为菱形,
为菱形,![]() 平面
平面![]() ,
,![]() ,
,
![]() 分别为
分别为![]() 的中点,
的中点,![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() .
.
(Ⅱ)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
参考答案:
【答案】.证明:(Ⅰ)∵四边形![]() 是菱形,
是菱形,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() , ∴
, ∴![]() .…………………2分
.…………………2分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]()
![]() .又∵
.又∵![]() ,
,
∴![]() 平面
平面![]() ,………………………………………4分
,………………………………………4分
又∵![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() . ………………………………6分
. ………………………………6分
(Ⅱ)解法一:由(1)知![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ………………………6分
………………………6分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
由(Ⅰ)知![]() ,又
,又![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .…………………………8分
.…………………………8分
∴平面![]() 是平面
是平面![]() 与平面
与平面![]() 的公垂面.
的公垂面.
所以,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的锐二面角的平面角.……9分
所成的锐二面角的平面角.……9分
在![]() 中,
中,![]() ,即
,即![]() .……………10分
.……………10分
又![]() ,
,
∴![]() .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .…………12分
.…………12分
理(Ⅱ)解法二:以![]() 为原点,
为原点,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正方向,
轴的正方向,
建立空间直角坐标系![]() ,如图.
,如图.
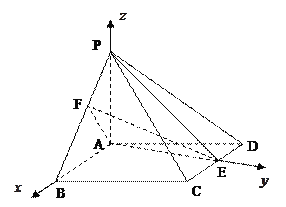
因为![]() ,
,![]() ,∴
,∴![]() 、
、![]() 、
、![]() 、
、![]() 6分
6分
则![]() ,
,![]() ,
,![]() .………7分
.………7分
由(Ⅰ)知![]() 平面
平面![]() ,
,
故平面![]() 的一个法向量为
的一个法向量为![]() .……………………8分
.……………………8分
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则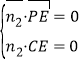 ,即
,即![]() ,令
,令![]() ,
,
则![]() . …………………10分
. …………………10分
∴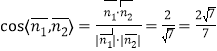 .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .……………12分
.……………12分
【解析】
试题分析:(Ⅰ)∵四边形![]() 是菱形,
是菱形,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() .
.
∴![]() ,即
,即![]() .
.
又![]() , ∴
, ∴![]() .…………………2分
.…………………2分
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]()
![]() .又∵
.又∵![]() ,
,
∴![]() 平面
平面![]() ,………………………………………4分
,………………………………………4分
又∵![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() . ………………………………6分
. ………………………………6分
(Ⅱ)解法一:由(1)知![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() ………………………7分
………………………7分
∵![]() 平面
平面![]() ,∴
,∴![]() .
.
由(Ⅰ)知![]() ,又
,又![]()
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .…………………………9分
.…………………………9分
∴平面![]() 是平面
是平面![]() 与平面
与平面![]() 的公垂面.
的公垂面.
所以,![]() 就是平面
就是平面![]() 与平面
与平面![]() 所成的锐二面角的平面角.……10分
所成的锐二面角的平面角.……10分
在![]() 中,
中,![]() ,即
,即![]() .……………11分
.……………11分
又![]() ,
,
∴![]() .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .…………14分
.…………14分
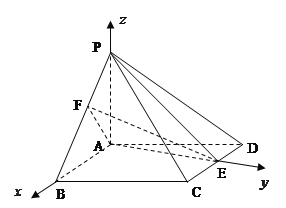
理(Ⅱ)解法二:以![]() 为原点,
为原点,![]() 、
、![]() 分别为
分别为![]() 轴、
轴、![]() 轴的正方向,建立空间直角坐标系
轴的正方向,建立空间直角坐标系![]() ,如图所示.因为
,如图所示.因为![]() ,
,![]() ,所以,
,所以,
![]() 、
、![]() 、
、![]() 、
、![]() ,…………7分
,…………7分
则![]() ,
,![]() ,
,![]() .………8分
.………8分
由(Ⅰ)知![]() 平面
平面![]() ,
,
故平面![]() 的一个法向量为
的一个法向量为![]() .……………………9分
.……………………9分
设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
则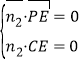 ,即
,即![]() ,令
,令![]() ,
,
则![]() . …………………11分
. …………………11分
∴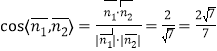 .
.
所以,平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]() .……14分
.……14分
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若f(-1)=f(1),求a,并直接写出函数
 的单调增区间;
的单调增区间;(2)当a≥
 时,是否存在实数x,使得
时,是否存在实数x,使得 =一
=一 ?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
?若存在,试确定这样的实数x的个数;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】通过对某城市一天内单次租用共享自行车的时间
 分钟到
分钟到 钟的
钟的 人进行统计,按照租车时间
人进行统计,按照租车时间 ,
,  ,
,  ,
,  ,
,  分组做出频率分布直方图,并作出租用时间和茎叶图(图中仅列出了时间在
分组做出频率分布直方图,并作出租用时间和茎叶图(图中仅列出了时间在 ,
,  的数据).
的数据).
(1)求
 的频率分布直方图中的
的频率分布直方图中的 ;
;(2)从租用时间在
 分钟以上(含
分钟以上(含 分钟)的人数中随机抽取
分钟)的人数中随机抽取 人,设随机变量
人,设随机变量 表示所抽取的
表示所抽取的 人租用时间在
人租用时间在 内的人数,求随机变量
内的人数,求随机变量 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆M::
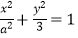 (a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(1)求椭圆方程;
(2)当直线l的倾斜角为45°时,求线段CD的长;
(3)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln(x+a)+x2
(1)若当x=﹣1时,f(x)取得极值,求a的值,并讨论f(x)的单调性;
(2)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于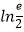 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,ADE是⊙O的割线,AC=AB,连接CD,CE,分别与⊙O交于点F,点G.

(1)求证:△ADC~△ACE;
(2)求证:FG∥AC. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,圆C的方程为
 (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(1)当m=3时,判断直线l与C的位置关系;
(2)当C上有且只有一点到直线l的距离等于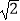 时,求C上到直线l距离为2
时,求C上到直线l距离为2 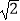 的点的坐标.
的点的坐标.
相关试题

