【题目】已知实数![]() ,函数
,函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最小值;
的最小值;
(2)当![]() 时,判断
时,判断![]() 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数![]() 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数![]() ,都存在以
,都存在以![]() 为边长的三角形.
为边长的三角形.
参考答案:
【答案】(1)2;(2)递增;(3).
【解析】
试题(1)研究函数问题,一般先研究函数的性质,如奇偶性,单调性,周期性等等,如本题中函数![]() 是偶函数,因此其最小值我们只要在
是偶函数,因此其最小值我们只要在![]() 时求得即可;(2)
时求得即可;(2)![]() 时,
时,![]() 可化简为
可化简为![]() ,下面我们只要按照单调性的定义就可证明在
,下面我们只要按照单调性的定义就可证明在![]() 上函数是单调递增的,当然在
上函数是单调递增的,当然在![]() 上是递减的;(3)处理此问题,首先通过换元法把问题简化,设
上是递减的;(3)处理此问题,首先通过换元法把问题简化,设![]() ,则函数
,则函数![]() 变为
变为![]() ,问题变为求实数
,问题变为求实数![]() 的范围,使得在区间
的范围,使得在区间![]() 上,恒有
上,恒有![]() .对于函数
.对于函数![]() ,我们知道,它在
,我们知道,它在![]() 上递减,在
上递减,在![]() 上递增,故我们要讨论它在区间
上递增,故我们要讨论它在区间![]() 上的最大(小)值,就必须分类讨论,分类标准显然是
上的最大(小)值,就必须分类讨论,分类标准显然是![]() ,
,![]() ,
,![]() ,在
,在![]() 时还要讨论最大值在区间
时还要讨论最大值在区间![]() 的哪个端点取得,也即共分成四类.
的哪个端点取得,也即共分成四类.
试题解析:易知![]() 的定义域为
的定义域为![]() ,且
,且![]() 为偶函数.
为偶函数.
(1)![]() 时,
时,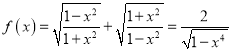
![]() 时
时![]() 最小值为2.
最小值为2.
(2)![]() 时,
时,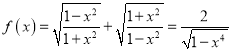
![]() 时,
时,![]() 递增;
递增;![]() 时,
时,![]() 递减;
递减;
![]() 为偶函数.所以只对
为偶函数.所以只对![]() 时,说明
时,说明![]() 递增.
递增.
设![]() ,所以
,所以![]() ,得
,得![]()
![]()
所以![]() 时,
时,![]() 递增;
递增;
(3)![]() ,
,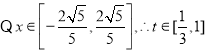 ,
,![]()
从而原问题等价于求实数![]() 的范围,使得在区间
的范围,使得在区间![]() 上,
上,
恒有![]() .
.
①当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() 由
由![]() 得
得![]() ,
,
从而![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
由![]() 得
得![]() ,从而
,从而![]() ;
;
③当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
由![]() 得
得![]() ,从而
,从而![]() ;
;
④当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
![]()
由![]() 得
得![]() ,从而
,从而![]() ;
;
综上,![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln(x+a)+x2
(1)若当x=﹣1时,f(x)取得极值,求a的值,并讨论f(x)的单调性;
(2)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于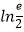 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,ADE是⊙O的割线,AC=AB,连接CD,CE,分别与⊙O交于点F,点G.

(1)求证:△ADC~△ACE;
(2)求证:FG∥AC. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,圆C的方程为
 (θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴,建立极坐标系,两种坐标系中取相同的单位长度,直线l的极坐标方程为ρcosθ+ρsinθ=m(m∈R).
(1)当m=3时,判断直线l与C的位置关系;
(2)当C上有且只有一点到直线l的距离等于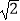 时,求C上到直线l距离为2
时,求C上到直线l距离为2 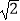 的点的坐标.
的点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知命题p:在△ABC中,若AB<BC,则sinC<sinA;命题q:已知a∈R,则“a>1”是“
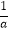 <1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
<1”的必要不充分条件.在命题p∧q,p∨q,(¬p)∨q,(¬p)∧q中,真命题个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子
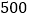 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子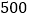 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过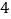 个直道与弯道的交接口
个直道与弯道的交接口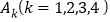 .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为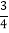 ,摔倒的概率均为
,摔倒的概率均为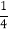 .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用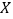 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.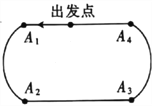
(1)求该运动员停止滑行时恰好已顺利通过
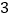 个交接口的概率;
个交接口的概率;(2)求
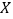 的分布列及数学期望
的分布列及数学期望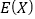 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的有( )
①函数y=
 的定义域为{x|x≥1};
的定义域为{x|x≥1};②函数y=x2+x+1在(0,+∞)上是增函数;
③函数f(x)=x3+1(x∈R),若f(a)=2,则f(-a)=-2;
④已知f(x)是R上的增函数,若a+b>0,则有f(a)+f(b)>f(-a)+f(-b).
A. 0个 B. 1个 C. 2个 D. 3个
相关试题

