【题目】已知椭圆M:: ![]() (a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(a>0)的一个焦点为F(﹣1,0),左右顶点分别为A,B.经过点F的直线l与椭圆M交于C,D两点.
(1)求椭圆方程;
(2)当直线l的倾斜角为45°时,求线段CD的长;
(3)记△ABD与△ABC的面积分别为S1和S2 , 求|S1﹣S2|的最大值.
参考答案:
【答案】
(1)解:因为F(﹣1,0)为椭圆的焦点,所以c=1,又b2=3,
所以a2=4,所以椭圆方程为 ![]() =1;
=1;
(2)解:因为直线的倾斜角为45°,所以直线的斜率为1,
所以直线方程为y=x+1,和椭圆方程联立得到
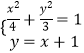 ,消掉y,得到7x2+8x﹣8=0,
,消掉y,得到7x2+8x﹣8=0,
所以△=288,x1+x2= ![]() ,x1x2=﹣
,x1x2=﹣ ![]() ,
,
所以|CD|= ![]() |x1﹣x2|=
|x1﹣x2|= ![]() ×
× ![]() =
= ![]() ;
;
(3)解:当直线l无斜率时,直线方程为x=﹣1,
此时D(﹣1, ![]() ),C(﹣1,﹣
),C(﹣1,﹣ ![]() ),△ABD,△ABC面积相等,|S1﹣S2|=0,
),△ABD,△ABC面积相等,|S1﹣S2|=0,
当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),
设C(x1,y1),D(x2,y2),
和椭圆方程联立得到 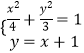 ,消掉y得(3+4k2)x2+8k2x+4k2﹣12=0,
,消掉y得(3+4k2)x2+8k2x+4k2﹣12=0,
显然△>0,方程有根,且x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() ,
,
此时|S1﹣S2|=2||y1|﹣|y2||=2|y1+y2|=2|k(x2+1)+k(x1+1)|
=2|k(x2+x1)+2k|= ![]() =
= ![]() ≤
≤ ![]() =
= ![]() =
= ![]() ,(k=
,(k= ![]() 时等号成立)
时等号成立)
所以|S1﹣S2|的最大值为 ![]()
【解析】(1)由焦点F坐标可求c值,根据a,b,c的平方关系可求得a值;(2)写出直线方程,与椭圆方程联立消掉y得关于x的一元二次方程,利用韦达定理及弦长公式即可求得|CD|;(3)当直线l不存在斜率时可得,|S1﹣S2|=0;当直线l斜率存在(显然k≠0)时,设直线方程为y=k(x+1)(k≠0),与椭圆方程联立消y可得x的方程,根据韦达定理可用k表示x1+x2 , x1x2 , |S1﹣S2|可转化为关于x1 , x2的式子,进而变为关于k的表达式,再用基本不等式即可求得其最大值;
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若A∪B=A,求实数m的取值范围;
(2)当x∈Z时,求A的非空真子集的个数;
(3)当x∈R时,若A∩B=,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)若f(-1)=f(1),求a,并直接写出函数
 的单调增区间;
的单调增区间;(2)当a≥
 时,是否存在实数x,使得
时,是否存在实数x,使得 =一
=一 ?若存在,试确定这样的实数x的个数;若不存在,请说明理由.
?若存在,试确定这样的实数x的个数;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】通过对某城市一天内单次租用共享自行车的时间
 分钟到
分钟到 钟的
钟的 人进行统计,按照租车时间
人进行统计,按照租车时间 ,
,  ,
,  ,
,  ,
,  分组做出频率分布直方图,并作出租用时间和茎叶图(图中仅列出了时间在
分组做出频率分布直方图,并作出租用时间和茎叶图(图中仅列出了时间在 ,
,  的数据).
的数据).
(1)求
 的频率分布直方图中的
的频率分布直方图中的 ;
;(2)从租用时间在
 分钟以上(含
分钟以上(含 分钟)的人数中随机抽取
分钟)的人数中随机抽取 人,设随机变量
人,设随机变量 表示所抽取的
表示所抽取的 人租用时间在
人租用时间在 内的人数,求随机变量
内的人数,求随机变量 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
如图,四棱锥
 的底面
的底面 为菱形,
为菱形, 平面
平面 ,
, ,
, 分别为
分别为 的中点,
的中点, .
.
(Ⅰ)求证:平面
 平面
平面 .
.(Ⅱ)求平面
 与平面
与平面 所成的锐二面角的余弦值.
所成的锐二面角的余弦值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=ln(x+a)+x2
(1)若当x=﹣1时,f(x)取得极值,求a的值,并讨论f(x)的单调性;
(2)若f(x)存在极值,求a的取值范围,并证明所有极值之和大于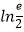 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的切线,ADE是⊙O的割线,AC=AB,连接CD,CE,分别与⊙O交于点F,点G.

(1)求证:△ADC~△ACE;
(2)求证:FG∥AC.
相关试题

