【题目】咖啡馆配制两种饮料,甲种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。乙种饮料分别用奶粉
。乙种饮料分别用奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。已知每天使用原料限额为奶粉
。已知每天使用原料限额为奶粉![]() 、咖啡
、咖啡![]() 、糖
、糖![]() 。如果甲种饮料每杯能获利
。如果甲种饮料每杯能获利![]() 元,乙种饮料每杯能获利
元,乙种饮料每杯能获利![]() 元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
参考答案:
【答案】每天应配制甲种饮料200杯,乙种饮料240杯,能使该咖啡馆获利最大
【解析】试题分析: 首先设每天应配制甲种饮料![]() 杯,乙种饮料
杯,乙种饮料![]() 杯,咖啡馆每天获利
杯,咖啡馆每天获利![]() 元,建立目标函数
元,建立目标函数![]() ,求出
,求出![]() 满足 的线性约束条件,画出可行域,找到最优解.
满足 的线性约束条件,画出可行域,找到最优解.
试题解析 :设每天配制甲种饮料![]() 杯,乙种饮料
杯,乙种饮料![]() 杯,咖啡馆每天获利
杯,咖啡馆每天获利![]() 元,则
元,则![]() 、
、![]() 满足约束条件:
满足约束条件:
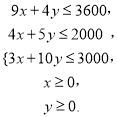
目标函数![]()
在平面直角坐标系内作出可行域,如图:
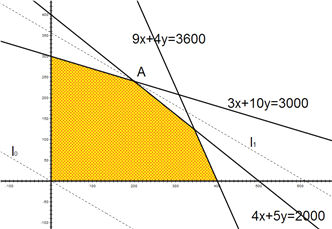
作直线![]() :
: ![]() ,把直线
,把直线![]() 向右上方平移至
向右上方平移至![]() 的位置时,直线经过可行域上的
的位置时,直线经过可行域上的![]() 点,且与原点距离最大,此时
点,且与原点距离最大,此时![]() 取最大值。
取最大值。
解方程组![]() ,得
,得![]() 点坐标
点坐标![]() 。
。
答:每天应配制甲种饮料200杯,乙种饮料240杯,能使该咖啡馆获利最大。
-
科目: 来源: 题型:
查看答案和解析>>【题目】有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人,则不同的安排方式共有__________种(用数字作答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
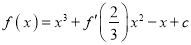 ,(其中
,(其中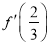 为
为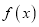 在点
在点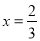 处的导数,
处的导数, 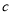 为常数).
为常数).(1)求
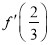 的值;
的值;(2)求函数
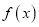 的单调区间;
的单调区间;(3)设函数
 ,若函数
,若函数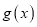 在区间
在区间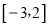 上单调递增,求实数
上单调递增,求实数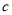 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在原点,离心率等于
的中心在原点,离心率等于 ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线 的焦点
的焦点(1)求椭圆
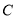 的方程;
的方程;(2)已知
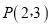 、
、 是椭圆上的两点,
是椭圆上的两点,  ,
, 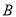 是椭圆上位于直线
是椭圆上位于直线 两侧的动点.①若直线
两侧的动点.①若直线 的斜率为
的斜率为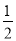 ,求四边形
,求四边形 面积的最大值;
面积的最大值;②当
 ,
,  运动时,满足
运动时,满足 ,试问直线
,试问直线 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由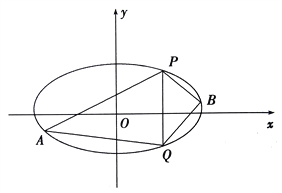
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值
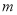
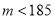
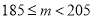
等级
三等品
二等品
一等品
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
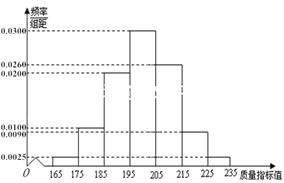
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值
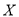 近似满足
近似满足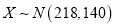 ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】要得到函数y=2cosxsin(x+
 )﹣
)﹣  的图象,只需将y=sinx的图象( )
的图象,只需将y=sinx的图象( )
A.先向左平移 个单位长度,再将所有点的横坐标缩短为原来的
个单位长度,再将所有点的横坐标缩短为原来的  倍(纵坐标不变)
倍(纵坐标不变)
B.先向左平移 个单位长度,再将所有点的横坐标缩短为原来的2倍(纵坐标不变)
个单位长度,再将所有点的横坐标缩短为原来的2倍(纵坐标不变)
C.先将所有点的横坐标缩短为原来的2倍(纵坐标不变),再向左平移 个单位长度
个单位长度
D.先将所有点的横坐标缩短为原来的 倍(纵坐标不变),再向左平移
倍(纵坐标不变),再向左平移  个单位长度
个单位长度 -
科目: 来源: 题型:
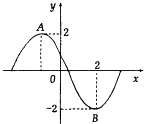
查看答案和解析>>【题目】函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象如图所示,其中A,B两点之间的距离为5,则f(x)的解析式是( )
A.y=2sin( x+
x+  )
)
B.y=2sin( x+
x+  )
)
C.y=2sin( x+
x+  )
)
D.y=2sin( x+
x+  )
)
相关试题

