【题目】已知函数![]() ,(其中
,(其中![]() 为
为![]() 在点
在点![]() 处的导数,
处的导数, ![]() 为常数).
为常数).
(1)求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)设函数![]() ,若函数
,若函数![]() 在区间
在区间![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围。
的取值范围。
参考答案:
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析: (1)对![]() 求导,令
求导,令![]() ,即可求出
,即可求出![]() ;(2)将
;(2)将![]() 代入
代入![]() 中,求导后,分别令
中,求导后,分别令![]() ,求出
,求出![]() 的范围,得到单调增区间,减区间;(3)由已知有
的范围,得到单调增区间,减区间;(3)由已知有![]() 恒成立,且
恒成立,且![]() ,得出
,得出![]() ,令
,令![]() ,由
,由![]() ,求出
,求出![]() 的范围.
的范围.
试题解析:(1)![]()
![]()
(2)![]()
![]()
当![]() ,即
,即![]() 或
或![]() 时,函数
时,函数![]() 单调递增;
单调递增;
当![]() ,即
,即![]() 时,函数
时,函数![]() 单调递减。
单调递减。
∴![]() 单调递增区间为
单调递增区间为![]() 和
和![]()
![]() 单调递减区间为
单调递减区间为![]()
(3)![]()
![]()
∵![]() 在区间
在区间![]() 上单调递增,
上单调递增,
∴![]()
![]() 恒成立.
恒成立.
∵![]() ∴
∴![]()
设![]() 则
则
 , ∴
, ∴![]() , ∴
, ∴![]()
答: ![]() 的取值范围是
的取值范围是![]() .
.
点睛:本题主要考查了导数的计算,导数在求函数单调性上的应用,属于中档题.求函数在某区间为增函数,一般转化为导函数大于或等于零问题.第三问另解: 得出![]() 恒成立,
恒成立, ![]() ,分离出常数
,分离出常数![]() ,即
,即![]() ,当
,当![]() 时,
时, ![]() 有最大值为11.所以
有最大值为11.所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
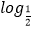 [
[ 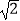 sin(x﹣
sin(x﹣  )].
)].
(1)求f(x)的定义域和值域;
(2)说明f(x)的奇偶性;
(3)求f(x)的单调增区间. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知f(x)=2x2﹣3x+1,g(x)=ksin(x﹣
 )(k≠0).
)(k≠0).
(1)设f(x)的定义域为[0,3],值域为A; g(x)的定义域为[0,3],值域为B,且AB,求实数k的取值范围.
(2)若方程f(sinx)+sinx﹣a=0在[0,2π)上恰有两个解,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有4位同学在同一天的上、下午参加“身高与体重”、“立定跳远”、“肺活量”、“握力”、“台阶”五个项目的测试,每位同学上、下午各测试一个项目,且不重复.若上午不测“握力”项目,下午不测“台阶”项目,其余项目上、下午都各测试一人,则不同的安排方式共有__________种(用数字作答).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
 的中心在原点,离心率等于
的中心在原点,离心率等于 ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线 的焦点
的焦点(1)求椭圆
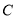 的方程;
的方程;(2)已知
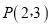 、
、 是椭圆上的两点,
是椭圆上的两点,  ,
,  是椭圆上位于直线
是椭圆上位于直线 两侧的动点.①若直线
两侧的动点.①若直线 的斜率为
的斜率为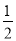 ,求四边形
,求四边形 面积的最大值;
面积的最大值;②当
 ,
,  运动时,满足
运动时,满足 ,试问直线
,试问直线 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由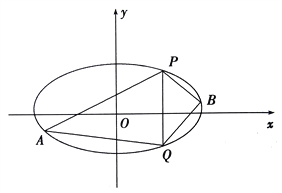
-
科目: 来源: 题型:
查看答案和解析>>【题目】咖啡馆配制两种饮料,甲种饮料分别用奶粉
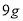 、咖啡
、咖啡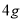 、糖
、糖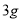 。乙种饮料分别用奶粉
。乙种饮料分别用奶粉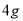 、咖啡
、咖啡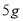 、糖
、糖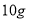 。已知每天使用原料限额为奶粉
。已知每天使用原料限额为奶粉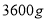 、咖啡
、咖啡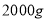 、糖
、糖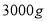 。如果甲种饮料每杯能获利
。如果甲种饮料每杯能获利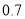 元,乙种饮料每杯能获利
元,乙种饮料每杯能获利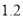 元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大?
元。每天在原料的使用限额内饮料能全部售出,每天应配制两种饮料各多少杯能获利最大? -
科目: 来源: 题型:
查看答案和解析>>【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
质量指标值
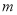
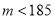
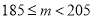
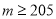
等级
三等品
二等品
一等品
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
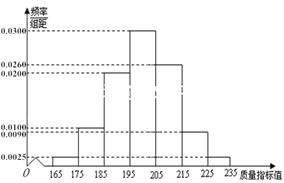
(Ⅰ)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品92%”的规定?
(Ⅱ)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(Ⅲ)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值
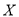 近似满足
近似满足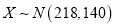 ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
相关试题

