【题目】已知函数f(x)= ![]() (a、b为常数),且f(1)=
(a、b为常数),且f(1)= ![]() ,f(0)=0.
,f(0)=0.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在定义域上的奇偶性,并证明;
(3)对于任意的x∈[0,2],f(x)(2x+1)<m4x恒成立,求实数m的取值范围.
参考答案:
【答案】
(1)解:由已知可得 ![]() ,
, ![]() ,
,
解得a=1,b=﹣1,
所以 ![]() ;
;
(2)函数f(x)为奇函数.
证明如下:f(x)的定义域为R,
∵ ![]() ,
,
∴函数f(x)为奇函数;
(3)解:∵ ![]() ,∴
,∴ ![]() ,
,
∴2x﹣1<m4x
∴ ![]() =g(x),
=g(x),
故对于任意的x∈[0,2],f(x)(2x+1)<m4x恒成立等价于m>g(x)max
令 ![]() ,则y=t﹣t2
,则y=t﹣t2 ![]() ,
,
则当 ![]() 时
时 ![]()
故 ![]() ,
,
即m的取值范围为 ![]() .
.
【解析】(1)运用代入法,得到a,b的方程,解得a,b,可得f(x)的解析式;(2)函数f(x)为奇函数.运用奇函数的定义,即可得证;(3)f(x)(2x+1)<m4x恒成立,即为2x﹣1<m4x , 运用参数分离和换元法,结合指数函数和二次函数的值域,可得右边的最大值,即可得到m的范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:全集U=R,函数
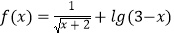 的定义域为集合A,集合B={x|x2﹣a<0}
的定义域为集合A,集合B={x|x2﹣a<0}
(1)求UA;
(2)若A∪B=A,求实数a的范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
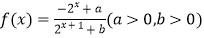 .
.
(1)当a=b=2时,证明:函数f(x)不是奇函数;
(2)设函数f(x)是奇函数,求a与b的值;
(3)在(2)条件下,判断并证明函数f(x)的单调性,并求不等式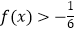 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f (x)=ex-ax-1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2-e)x.
①求函数h(x)=f (x)-g (x)的单调区间;
②若函数
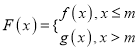 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;(2)若存在实数x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求证:e-1≤a≤e2-e.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=x2+mx﹣4在区间[﹣2,1]上的两个端点处取得最大值和最小值.
(1)求实数m的所有取值组成的集合A;
(2)试写出f(x)在区间[﹣2,1]上的最大值g(m);
(3)设h(x)=﹣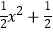 x+7,令F(m)=
x+7,令F(m)= 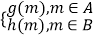 ,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围.
,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:
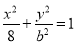 经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).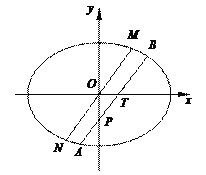
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求
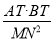 的值;
的值;(3)记直线l与y轴的交点为P.若
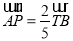 ,求直线l的斜率k.
,求直线l的斜率k. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
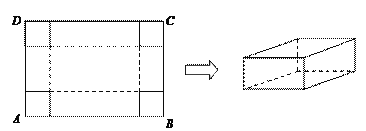
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
相关试题

