【题目】已知函数f(x)=x2+mx﹣4在区间[﹣2,1]上的两个端点处取得最大值和最小值.
(1)求实数m的所有取值组成的集合A;
(2)试写出f(x)在区间[﹣2,1]上的最大值g(m);
(3)设h(x)=﹣ ![]() x+7,令F(m)=
x+7,令F(m)= ![]() ,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围.
,其中B=RA,若关于m的方程F(m)=a恰有两个不相等的实数根,求实数a的取值范围.
参考答案:
【答案】
(1)解:∵f(x)=x2+mx﹣4在区间[﹣2,1]上的两个端点处取得最大值和最小值,
∴函数在区间[﹣2,1]上是单调函数,
又∵函数f(x)的图象为开口向上的抛物线,对称轴为x=﹣ ![]()
∴必有﹣ ![]() ≥1,或﹣
≥1,或﹣ ![]() ≤﹣2,解得m≥4或 m≤﹣2,
≤﹣2,解得m≥4或 m≤﹣2,
∴实数m的所有取值组成的集合A={m|m≥4或 m≤﹣2}
(2)解:当 m≥4时,﹣ ![]() ≤﹣2,函数f(x)在区间[﹣2,1]上单调递增,
≤﹣2,函数f(x)在区间[﹣2,1]上单调递增,
∴函数f(x)的最大值g(m)=f(1)=m﹣3;
当m≤﹣2 时,﹣ ![]() ≥1,函数f(x)在区间[﹣2,1]上单调递减,
≥1,函数f(x)在区间[﹣2,1]上单调递减,
∴函数f(x)的最大值g(m)=f(﹣2)=﹣2m
(3)解:由题意可知F(m)= 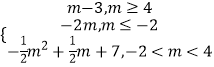 ,
,
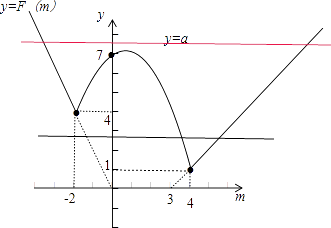
关于m的方程F(m)=a恰有两个不相等的实数根等价于y=F(m)的图象与y=a的图象有两个不同的交点,
作图可知实数a的取值范围为:a> ![]() 或1<a<4
或1<a<4
【解析】(1)问题等价于函数在区间[﹣2,1]上是单调函数,由二次函数可得﹣ ![]() ≥1,或﹣
≥1,或﹣ ![]() ≤﹣2,解得不等式即可;(2)分类讨论结合单调性可得:当 m≥4时g(m)=f(1)=m﹣3,当m≤﹣2时g(m)=f(﹣2)=﹣2m.(3)由题意可知F(m)=
≤﹣2,解得不等式即可;(2)分类讨论结合单调性可得:当 m≥4时g(m)=f(1)=m﹣3,当m≤﹣2时g(m)=f(﹣2)=﹣2m.(3)由题意可知F(m)= 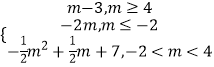 ,问题等价于y=F(m)的图象与y=a的图象有两个不同的交点,数形结合易得答案.
,问题等价于y=F(m)的图象与y=a的图象有两个不同的交点,数形结合易得答案.
【考点精析】通过灵活运用集合的补集运算和二次函数在闭区间上的最值,掌握对于全集U的一个子集A,由全集U中所有不属于集合A的所有元素组成的集合称为集合A相对于全集U的补集,简称为集合A的补集,记作:CUA即:CUA={x|x∈U且x∈A};补集的概念必须要有全集的限制;当![]() 时,当
时,当![]() 时,
时,![]() ;当
;当![]() 时在
时在![]() 上递减,当
上递减,当![]() 时,
时,![]() 即可以解答此题.
即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
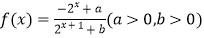 .
.
(1)当a=b=2时,证明:函数f(x)不是奇函数;
(2)设函数f(x)是奇函数,求a与b的值;
(3)在(2)条件下,判断并证明函数f(x)的单调性,并求不等式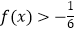 的解集.
的解集. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f (x)=ex-ax-1,其中e为自然对数的底数,a∈R.
(1)若a=e,函数g (x)=(2-e)x.
①求函数h(x)=f (x)-g (x)的单调区间;
②若函数
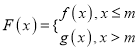 的值域为R,求实数m的取值范围;
的值域为R,求实数m的取值范围;(2)若存在实数x1,x2∈[0,2],使得f(x1)=f(x2),且|x1-x2|≥1,
求证:e-1≤a≤e2-e.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
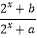 (a、b为常数),且f(1)=
(a、b为常数),且f(1)=  ,f(0)=0.
,f(0)=0.
(1)求函数f(x)的解析式;
(2)判断函数f(x)在定义域上的奇偶性,并证明;
(3)对于任意的x∈[0,2],f(x)(2x+1)<m4x恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,焦点在x轴上的椭圆C:
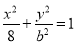 经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).
经过点(b,2e),其中e为椭圆C的离心率.过点T(1,0)作斜率为k(k>0)的直线l交椭圆C于A,B两点(A在x轴下方).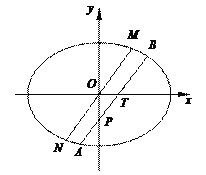
(1)求椭圆C的标准方程;
(2)过点O且平行于l的直线交椭圆C于点M,N,求
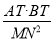 的值;
的值;(3)记直线l与y轴的交点为P.若
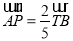 ,求直线l的斜率k.
,求直线l的斜率k. -
科目: 来源: 题型:
查看答案和解析>>【题目】在一张足够大的纸板上截取一个面积为3600平方厘米的矩形纸板ABCD,然后在矩形纸板的四个角上切去边长相等的小正方形,再把它的边沿虚线折起,做成一个无盖的长方体纸盒(如图).设小正方形边长为x厘米,矩形纸板的两边AB,BC的长分别为a厘米和b厘米,其中a≥b.
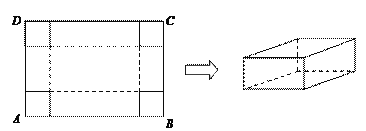
(1)当a=90时,求纸盒侧面积的最大值;
(2)试确定a,b,x的值,使得纸盒的体积最大,并求出最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比赛得分的情况用如图所示的茎叶图表示,则甲、乙两名运动员的中位数分别为( )
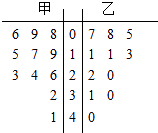
A.19、13
B.13、19
C.20、18
D.18、20
相关试题

